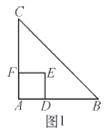
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF; ②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.


参考答案:
【答案】(1) BD=CF成立,证明见解析;(2)①证明见解析;②FG=![]() .
.
【解析】试题分析:(1)证明线段相等的常用方法是三角形的全等,直观上判 断BD=CF,而由题目条件,旋转过程中出
现了两个三角形△BAD和△CAF,并且包含了要证明相等的两条线段BD和CF,∵△ABC是等腰直角三角形,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,只差夹角相等,在Rt△BAC中,∠BAD+∠DAC=90°,∠CAF+∠DAC="90°," ∴∠BAD="∠CAF," ∴△BAD≌△CAF, BD=CF.(2)①要证明BD⊥CF,只要证明∠BGC=90°,即∠GBC+∠BCG=∠GBC+∠ACF+∠ACB=90°,在Rt△BAC中,∠ABC+
∠ACB=∠ABG+∠GBC+∠BCA=90°,有(1)知,∠ACF=∠ABG,所以∠GBC+∠ACF+∠ACB=∠GBC+
∠ABG +∠ACB =90°,所以BD⊥CF.②求线段的方法一般是三角形的全等和勾股定理,题目中没有和FG直接相关的线段,而CG从已知条件中又无法求出,所以需要作辅助线,连接FD,交AC于点N, 在正方形ADEF中,AD=DE=![]() , AN="1," CN=3,由勾股定理CF=
, AN="1," CN=3,由勾股定理CF=![]() ,设FG=x,CG=
,设FG=x,CG=![]() ,在Rt△FGD中,∵FD=2,∴GD=
,在Rt△FGD中,∵FD=2,∴GD=![]() ,∵在Rt△BCG中,
,∵在Rt△BCG中,![]() ,
,
∴![]() ,解之得FG=
,解之得FG=![]() .
.
试题解析:②解法一:
如图,连接FD,交AC于点N,
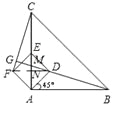
∵在正方形ADEF中,AD=DE=![]() ,
,
∴AN=FN=![]() AE=1,FD=2,
AE=1,FD=2,
∵在等腰直角△ABC 中,AB=4,∴CN=AC-AN=3,
∴在Rt△FCN中,![]() ,
,
∵△BAD≌△CAF(已证),∴BD=CF=![]() ,
,
设FG=![]() ,在Rt△FGD中,∵FD=2,∴GD=
,在Rt△FGD中,∵FD=2,∴GD=![]() ,
,
∵CF=![]() ,∴CG=
,∴CG=![]() ,
,
∵在等腰直角△ABC 中,AB=AC=4,
∴![]() ,
,
∵在Rt△BCG中,![]() ,
,
∴![]() ,
,
整理,得![]() ,
,
解之,得![]() ,
,![]() (不合题意,故舍去)
(不合题意,故舍去)
∴FG=![]() .
.
解法二:
如图,连接FD,交AC于点N;连接CD,
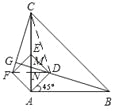
同解法一,可得:DG=![]() ,CG=
,CG=![]() ,
,
易证△ACD≌△ABD(SAS),可得CD=BD=![]() ,
,
在Rt△CGD中,![]() ,即
,即![]()
解之,得![]() ,故FG=
,故FG=![]() .
.
-
科目: 来源: 题型:
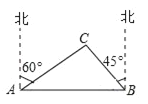
查看答案和解析>>【题目】某市在新农村改造工程中需要修建一段东西方向全长1000米的道路(记作AB).已知C点周围350米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(
 ≈1.732,
≈1.732, ≈1.414)
≈1.414)(1)道路AB是否穿过电力设施区域?为什么?
(2)在施工250米后,为了尽量减少施工对城市交通所造成的影响,加快了施工进度,实际工作效率变成了原计划工作效率的1.5倍,结果提前5天完成了修路任务,则原计划每天修路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求出售价x的范围;
(3)商场每月销售这种空气净化器所获得的利润为w(元),写出w关于x的关系?当售价x(元/台)定为多少时利润最大,最大是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求
 的长度.(结果保留π)
的长度.(结果保留π)
-
科目: 来源: 题型:
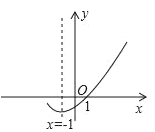
查看答案和解析>>【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①abc<0;②b>2a;③a+b+c=0;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.
其中正确的命题有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
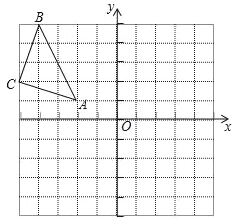
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
相关试题

