搜索
【题目】如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：
①abc＜0；②b＞2a；③a+b+c=0；④8a+c＞0；⑤ax2+bx+c=0的两根分别为﹣3和1．
其中正确的命题有（ ）
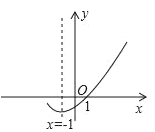
A. 2个 B. 3个 C. 4个 D. 5个
参考答案：
【答案】C
【解析】解：①∵开口向上，∴a＞0，对称轴在y轴的左侧，b＞0，抛物线与y轴交于负半轴，c＜0，∴abc＜0，∴①正确；
②
=﹣1，b=2a，②错误；
③当x=1时，y=0，∴a+b+c=0，③正确；
④当x=2时，y＞0，∴4a+2b+c＞0，∴8a+c＞0，④正确；
⑤∵对称轴为x=﹣1，抛物线与x轴的交点坐标分别为（﹣3，0），（1，0），∴ax2+bx+c=0的两根分别为﹣3和1，⑤正确．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．
（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；
（2）求出售价x的范围；
（3）商场每月销售这种空气净化器所获得的利润为w（元），写出w关于x的关系？当售价x（元/台）定为多少时利润最大，最大是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OA，OD是⊙O半径．过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B．
(1)求证：直线CD是⊙O的切线；
(2)如果D点是BC的中点，⊙O的半径为 3cm，求
的长度．(结果保留π)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，点D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G.
①求证：BD⊥CF； ②当AB=4，AD=
时，求线段BG的长.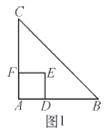
-
科目： 来源： 题型：
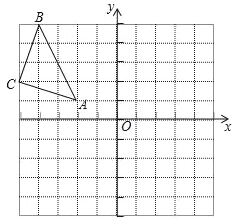
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣4，5），C（﹣5，2）．
（1）画出△ABC关于原点O成中心对称的△A1B1C1；
（2）写出△A1B1C1的顶点坐标；
（3）求出△A1B1C1的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的推理．
如图，BE平分∠ABD，DE平分∠BDC，且∠α＋∠β＝90°，试说明：AB∥CD.
完成推理过程：
∵BE平分∠ABD(已知)，
∴∠ABD＝2∠α(__________)．
∵DE平分∠BDC(已知)，
∴∠BDC＝2∠β (__________)．
∴∠ABD＋∠BDC＝2∠α＋2∠β＝2(∠α＋∠β)( __________)．
∵∠α＋∠β＝90°(已知)，
∴∠ABD＋∠BDC＝180°(__________)．
∴AB∥CD(____________________)．
-
科目： 来源： 题型：
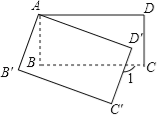
查看答案和解析>>【题目】如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
相关试题
