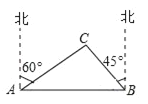
【题目】某市在新农村改造工程中需要修建一段东西方向全长1000米的道路(记作AB).已知C点周围350米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
(1)道路AB是否穿过电力设施区域?为什么?
(2)在施工250米后,为了尽量减少施工对城市交通所造成的影响,加快了施工进度,实际工作效率变成了原计划工作效率的1.5倍,结果提前5天完成了修路任务,则原计划每天修路多少米?
参考答案:
【答案】(1)不穿过;(2)50.
【解析】试题分析:(1)首先过点C作CD⊥AB于点D,设CD=x米,然后利用三角函数,即可表示出AD与BD的长,继而可得方程![]() x+x=1000,求得CD的长,与350米比较,即可得道路AB不穿过电力设施区域;
x+x=1000,求得CD的长,与350米比较,即可得道路AB不穿过电力设施区域;
(2)首先设原计划每天修路y米,根据题意即可得分式方程,解分式方程即可求得答案.
试题解析:解:(1)道路AB不穿过电力设施区域.
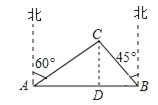
如图,过点C作CD⊥AB于点D,设CD=x米.由题意得:∠CAD=90°﹣60°=30°,∠CBD=90°﹣45°=45°.在Rt△ACD中,AD=![]() =
= ![]() (米).在Rt△BCD中,BD=CD=x(米).∵AB=1000米,∴
(米).在Rt△BCD中,BD=CD=x(米).∵AB=1000米,∴![]() x+x=1000,解得:x=500
x+x=1000,解得:x=500![]() ﹣500≈366.∵366米>350米,∴道路AB不穿过电力设施区域;
﹣500≈366.∵366米>350米,∴道路AB不穿过电力设施区域;
(2)设原计划每天修路y米,依题意得:
![]()
解得:y=50,经检验,y=50是原分式方程的解.
答:原计划每天修路50米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)解方程组:
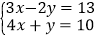 .
.(2)解不等式组
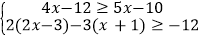 (并把解集在数轴上表示出来).
(并把解集在数轴上表示出来). -
科目: 来源: 题型:
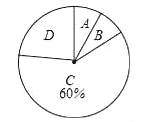
查看答案和解析>>【题目】今年10月,某公司随机抽取所属的a家连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.

根据以上信息解答下列问题:
(1)求a的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年4月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况. 我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:

(1)请将两幅图补充完整;
(2)在这次形体测评中,一共抽查了______名学生,如果全市有20万名初中生,那么全市初中生中,三姿良好的学生约有______人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求出售价x的范围;
(3)商场每月销售这种空气净化器所获得的利润为w(元),写出w关于x的关系?当售价x(元/台)定为多少时利润最大,最大是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求
 的长度.(结果保留π)
的长度.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF; ②当AB=4,AD=
 时,求线段BG的长.
时,求线段BG的长.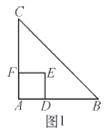


相关试题

