【题目】在平面直角坐标系中,点A(m,n)在第一象限内,m,n均为整数,且满足![]() .
.
(1)求点A的坐标;
(2)将线段OA向下平移a(a>0)个单位后得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点B,若
轴于点B,若![]() ,求a的值;
,求a的值;
(3)过点A向x轴作垂线,垂足为点C,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点C出发,以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,当![]() 时,判断四边形AMON的面积
时,判断四边形AMON的面积![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
参考答案:
【答案】(1)点A的坐标为(3,2);(2)![]() ;(3)四边形AMON的面积是定值3,理由见解析
;(3)四边形AMON的面积是定值3,理由见解析
【解析】
(1)根据题意求出n的解集,即可解答
(2)根据题意可分期款讨论:当点B在原点O的上方时,![]() ;当点B在原点O的下方时,
;当点B在原点O的下方时,![]()
(3)过点A向y轴作垂线,垂足为A`,得到C(3,0),m(0,2t),n(3-3t),A`(0,2)
,再利用![]() ,即可解答
,即可解答
(1)∵![]()
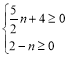
解之,得![]()
∵![]() ,且n为正整数
,且n为正整数
∴![]()
又∵m为正整数
∴n=2,m=3
故点A的坐标为(3,2)
(2)平移后:![]()
当点B在原点O的上方,如图1:
∵![]()
∴(2-a)-(-a)=3(2-a)
∴![]()
当点B在原点O的下方,如图2:
∵![]()
∴(2-a)-(-a)=3(2-a)
∴![]()
故![]()
(3)如图3,过点A向y轴作垂线,垂足为A`,则
C(3,0),m(0,2t),n(3-3t),A`(0,2)
![]()
=2![]()
=6-3-3t+3t
=3
故四边形AMON的面积是定值3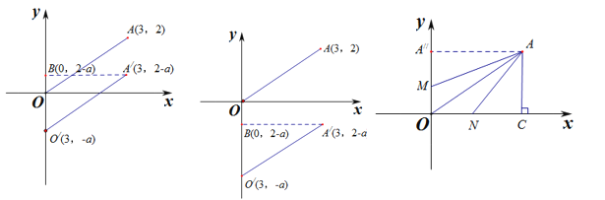
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:
次数
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
频数
a
4
12
16
8
3
结合图表完成下列问题:
(1)a= ,全班人数是______;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀学生人数占全班总人数的百分之几?

-
科目: 来源: 题型:
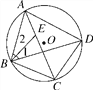
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
(1)判断BE与⊙O的位置关系,并说明理由;
(2)若∠ACB=30°,⊙O的半径为4,请求出图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(2,1),B(﹣1,1),C(﹣1,﹣3),D(2,﹣3),点P从点A出发,以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A…的规律在图边形ABCD的边上循环运动,则第2019秒时点P的坐标为( )

A. (1,1)B. (0,1)C. (﹣1,1)D. (2,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,在矩形ABCD中,AB=5,AD=
 ,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF
,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值;
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是x元,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1000元.
(1)若某日的净收入为5000元,且使游客得到实惠,则当天的观光车的日租金是多少元?(注:净收入=租车收入-管理费)
(2)设每日净收入为w元,请写出w与x之间的函数关系式;并求出日租金为多少时,每日净收入最大?
相关试题

