搜索
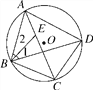
【题目】如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC＝BC＝DC.
(1)若∠CBD＝39°，求∠BAD的度数；
(2)求证：∠1＝∠2.
参考答案：
【答案】（1）78°（2）证明见解析
【解析】试题分析：（1）根据等腰三角形的性质由BC=DC得到∠CBD=∠CDB=39°，再根据圆周角定理得∠BAC=∠CDB=39°，∠CAD=∠CBD=39°，所以∠BAD=∠BAC+∠CAD=78°；
（2）根据等腰三角形的性质由EC=BC得∠CEB=∠CBE，再利用三角形外角性质得∠CEB=∠2+∠BAE，则∠2+∠BAE=∠1+∠CBD，加上∠BAE=∠CBD，所以∠1=∠2．
（1）解：∵BC=DC，
∴∠CBD=∠CDB=39°，
∵∠BAC=∠CDB=39°，∠CAD=∠CBD=39°，
∴∠BAD=∠BAC+∠CAD=39°+39°=78°；
（2）证明：∵EC=BC，
∴∠CEB=∠CBE，
而∠CEB=∠2+∠BAE，∠CBE=∠1+∠CBD，
∴∠2+∠BAE=∠1+∠CBD，
∵∠BAE=∠BDC=∠CBD，
∴∠1=∠2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，
，点E在AD上，且
，连接EC，将矩形ABCD沿直线BE翻折，点A恰好落在EC上的点A'处，则
____________cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD 的边长为4，E 为AB 上一点，且AE=3 ，F 为BC 边上的一个动点，连接EF ，以EF 为边向左侧作等腰直角三角形FEG ，EG=EF，∠GEF=90°，连接AG ，则AG 的最小值为________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校七（1）班体育委员统计了全班同学60秒跳绳的次数，并绘制出如下频数分布表和频数分布直方图：
次数
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
频数
a
4
12
16
8
3
结合图表完成下列问题：
（1）a= ，全班人数是______；
（2）补全频数分布直方图；
（3）若跳绳次数不少于140的学生成绩为优秀，则优秀学生人数占全班总人数的百分之几？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD内接于⊙O，AC是⊙O的直径，过点B作BE⊥AD，垂足为点E，AB平分∠CAE．
（1）判断BE与⊙O的位置关系，并说明理由；
（2）若∠ACB=30°，⊙O的半径为4，请求出图中阴影部分的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点A（m，n）在第一象限内，m，n均为整数，且满足
.（1）求点A的坐标；
（2）将线段OA向下平移a（a>0）个单位后得到线段
，过点
作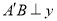
轴于点B，若
，求a的值；（3）过点A向x轴作垂线，垂足为点C，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点C出发，以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，当
时，判断四边形AMON的面积
的值是否变化？若不变，求出其值；若变化，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A（2，1），B（﹣1，1），C（﹣1，﹣3），D（2，﹣3），点P从点A出发，以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A…的规律在图边形ABCD的边上循环运动，则第2019秒时点P的坐标为（ ）
A. （1，1）B. （0，1）C. （﹣1，1）D. （2，﹣1）
相关试题
