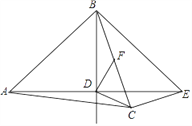
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
参考答案:
【答案】(1)BC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)利用勾股定理求出BE的长,进而再次利用勾股定理求出BC的长;
(2)连接AF,首先利用ASA证明出△BDF≌△EDC,得到![]() ,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
试题解析:(1)∵BD⊥AD,点E在AD的延长线上,
∴![]()
∵![]()
∴![]()
∵BC⊥CE,
∴![]()
∴![]()
(2)连接AF,

∵CD⊥BD,DF⊥CD,
∴![]()
∴∠BDF=∠CDE,
∵CE⊥BC,
∴![]()
∴∠DBC=∠CED,
在△BDF和△EDC中,
∵
∴△BDF≌△EDC(ASA),
∴DF=CD,
∴![]()
∵∠ADB=∠CDF,
∴∠ADB+∠BDF=∠CDF+∠BDF,
∴∠ADF=∠BDC,
在△ADF和△BDC中,
∵
∴△ADF≌△BDC(SAS),
∴∠AFD=∠BCD,
∴![]()
∴![]()
∴AF⊥BC,
∴AB=AC,
∴BF=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一快递员需要在规定时间内开车将快递送到某地,若快递员开车每分钟行驶1.2
 ,就早到10分钟;若快递员开车每分钟行驶0.8
,就早到10分钟;若快递员开车每分钟行驶0.8 ,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.小明和小新在解答时先设出未知数,然后列出方程如下:
 ①,
①, ②,其中方程①由小明所列,方程②由小新所列.
②,其中方程①由小明所列,方程②由小新所列.(1)小明所设
 表示 ;
表示 ;小新所设
 表示 .
表示 .(2)请选小明或小新的方法写出完整的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
 =
= 与反比例函数
与反比例函数 =
= 的图像有一个交点
的图像有一个交点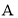 (
( ,3),
,3), ⊥
⊥ 轴于点
轴于点 ,平移直线
,平移直线 =
= ,使其经过点
,使其经过点 ,得到直线
,得到直线 ,则直线
,则直线 对应的函数解析式是_____________.
对应的函数解析式是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级同学到距离学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往目的地。如图,
 ,
, 分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )
分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )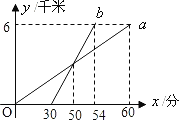
A. 骑车的同学比步行的同学晚出发30分钟 B. 步行的速度是6千米/小时
C. 骑车同学从出发到追上步行同学用了20分钟 D. 骑车同学和步行的同学同时到达目的地
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了有理数的加减法之后,老师讲解了例题
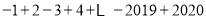 的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.根据这个思路学生改编了下列几题:
(1)计算:①

②

(2)蚂蚁在数轴的原点
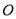 处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……①按照这个规律,第1024次爬行后蚂蚁所在位置在原点左侧还是右侧?对应哪个数?
②按照这个规律,第 次爬行后蚂蚁在数轴上表示751的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=
 x2+
x2+ x﹣
x﹣ 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y=
 x2+
x2+ x﹣
x﹣ 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方错误的是( )
A. x2+2x﹣99=0化为(x+1)2=100
B. 2x2﹣7x﹣4=0化为
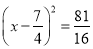
C. x2+8x+9=0化为(x+4)2=25
D. 3x2﹣4x﹣2=0化为(x-
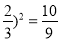
相关试题

