【题目】在学习了有理数的加减法之后,老师讲解了例题![]() 的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
根据这个思路学生改编了下列几题:
(1)计算:①![]()
②![]()
(2)蚂蚁在数轴的原点![]() 处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
①按照这个规律,第1024次爬行后蚂蚁所在位置在原点左侧还是右侧?对应哪个数?
②按照这个规律,第 次爬行后蚂蚁在数轴上表示751的位置.
参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)①第1024次爬行后蚂蚁所在位置在原点左侧,对应-1024,②750.
;(2)①第1024次爬行后蚂蚁所在位置在原点左侧,对应-1024,②750.
【解析】
(1)①由每两个数为一组、其和为-1,共1010组,据此可得;
②由每两个数为一组、其和为-2,共505组,据此求解可得;
(2)①根据题意列出算式:1+2-3-4+5+6-7-8+9+10-11-12+……+1021+1022-1023-1024,每四个数为一组、其和为-4,共256组,据此求解可得.
②找到小蚂蚁在正半轴爬行的规律,据此解答即可.
(1)①![]() =-1×1010=-1010;
=-1×1010=-1010;
②1-3+5-7+……+2017-2019=-2×505=-1010;
(2)①![]()
=![]()
=-4×256
=-1024
所以第1024次爬行后蚂蚁所在位置在原点左侧,对应-1024.
②小蚂蚁在正半轴爬行的规律为:第5次爬行到表示1的位置,第6次爬行到表示1+6=7的位置;第9次爬行到表示1的位置,第10次爬行到表示1+10=11的位置;第13次爬行到表示1的位置,第14次爬行到表示1+14=15的位置,故小蚂蚁爬行第(4n+1)次均在表示1的位置,,749=187×4+1,故第749次爬行到表示1的位置,第750次爬行到表示1+750=751的位置.
故答案为:750
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
 =
= 与反比例函数
与反比例函数 =
= 的图像有一个交点
的图像有一个交点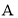 (
( ,3),
,3), ⊥
⊥ 轴于点
轴于点 ,平移直线
,平移直线 =
= ,使其经过点
,使其经过点 ,得到直线
,得到直线 ,则直线
,则直线 对应的函数解析式是_____________.
对应的函数解析式是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级同学到距离学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往目的地。如图,
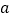 ,
, 分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )
分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )
A. 骑车的同学比步行的同学晚出发30分钟 B. 步行的速度是6千米/小时
C. 骑车同学从出发到追上步行同学用了20分钟 D. 骑车同学和步行的同学同时到达目的地
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
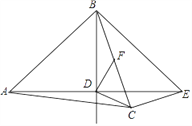
(1)若BD=DE=
 ,CE=
,CE=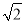 ,求BC的长;
,求BC的长; (2)若BD=DE,求证:BF=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=
 x2+
x2+ x﹣
x﹣ 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y=
 x2+
x2+ x﹣
x﹣ 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方错误的是( )
A. x2+2x﹣99=0化为(x+1)2=100
B. 2x2﹣7x﹣4=0化为
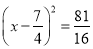
C. x2+8x+9=0化为(x+4)2=25
D. 3x2﹣4x﹣2=0化为(x-
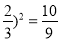
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=4,BC=12,点E是BC的中点.点P、Q分别是边AD、BC上的两点,其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A,同时点Q以每秒2个单位长度的速度从点C出发向点B运动.当其中一点到达终点时停止运动.当运动时间t为_____秒时,以点A、P,Q,E为顶点的四边形是平行四边形.

相关试题

