【题目】如图,已知二次函数y=![]() x2+
x2+![]() x﹣
x﹣![]() 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y=![]() x2+
x2+![]() x﹣
x﹣![]() 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)顶点D的坐标为(﹣1,﹣![]() ),直线AC的解析式为y=﹣
),直线AC的解析式为y=﹣![]() x﹣
x﹣![]() ;(2)当t=﹣
;(2)当t=﹣![]() 时,△PEC的面积最大,最大值是
时,△PEC的面积最大,最大值是![]() ,此时,点P的坐标为(﹣
,此时,点P的坐标为(﹣![]() ,﹣
,﹣![]() );(3)存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1,
);(3)存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1, ![]() )(﹣1,
)(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() ).
).
【解析】试题分析:(1)根据配方法,可得顶点坐标,根据自变量与函数值的对应关系,可得答案,根据待定系数法,可得函数解析式;
(2)根据线段垂直平分线的性质,线段的性质,可得E的坐标,根据平行于y的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PQ,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;
(3)根据勾股定理,可得关于d的方程,根据解方程,可得答案.
试题解析:
(1)y=![]() x2+
x2+![]() x﹣
x﹣![]() =
=![]() (x+1)2﹣
(x+1)2﹣![]() ,顶点D的坐标为(﹣1,﹣
,顶点D的坐标为(﹣1,﹣![]() ),
),
当y=0时, ![]() x2+
x2+![]() x﹣
x﹣![]() =0,解得x1=﹣3,x2=1,
=0,解得x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0).
当x=0时,y=﹣![]() ,
,
∴C(0,﹣![]() ),
),
∴直线AC的解析式为y=﹣![]() x﹣
x﹣![]()
(2)∵△CPE得周长为BC+CE+BE,其中BC的长是固定的,
∴周长取得最小值就是BE+CE取得最小值,
∵点E是抛物线对称轴上一点,
∴BE=AE,
∴BE+CE=AE+CE,
∴BE+CE的最小值是AC,点E是AC与对称轴的交点.
∴点E为(﹣1,﹣![]() ).
).
∵点P是抛物线上x轴下方一点,设点P为(t, ![]() t2+
t2+![]() t﹣
t﹣![]() ).且
).且![]() t2+
t2+![]() t﹣
t﹣![]() <0.
<0.
过点P作QP⊥x轴交直线AC于点Q,点Q坐标为(t,﹣![]() t﹣
t﹣![]() ).
).
当点p在对称轴左侧时,S△PCE=S△PCQ﹣S△PEQ=![]() PQ(0﹣t)﹣
PQ(0﹣t)﹣![]() PQ(﹣1﹣t)=
PQ(﹣1﹣t)=![]() PQ,
PQ,
当点P在对称轴的右侧时,S△PCE=S△PCQ+S△PEQ=![]() PQ(0﹣t)+
PQ(0﹣t)+![]() PQ[t﹣(﹣1)]=
PQ[t﹣(﹣1)]= ![]() PQ,
PQ,
∵PQ=(﹣![]() t﹣
t﹣![]() )﹣(
)﹣(![]() t2+
t2+![]() t﹣
t﹣![]() )=﹣
)=﹣![]() t2﹣
t2﹣![]() t,
t,
∴S△PCE=![]() PQ=﹣
PQ=﹣![]() t2﹣
t2﹣![]() t=﹣
t=﹣![]() (t+
(t+![]() )2+
)2+![]() .
.
当t=﹣![]() 时,△PEC的面积最大,最大值是
时,△PEC的面积最大,最大值是![]() ,此时,点P的坐标为(﹣
,此时,点P的坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)经过点P且平行于AC的直线MN的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
当x=0时,y=-![]() ,即N(0,﹣
,即N(0,﹣![]() ),当y=0时,x=﹣
),当y=0时,x=﹣![]() ,即M(﹣
,即M(﹣![]() ,0),
,0),
设点D′的坐标为(﹣1,d),则MN2=(﹣![]() )2+(﹣
)2+(﹣![]() )2=
)2=![]() ,MD′2=[﹣
,MD′2=[﹣![]() ﹣(﹣1)]2+d2=
﹣(﹣1)]2+d2=![]() +d2,ND′2=(﹣1)2+(﹣
+d2,ND′2=(﹣1)2+(﹣![]() ﹣d)2=d2+
﹣d)2=d2+![]() d+
d+![]() .
.
当∠MD′N=90°时,MD′2+ND′2=MN2,即![]() +d2+d2+
+d2+d2+![]() d+
d+![]() =
=![]() ,
,
整理,得4d2+7![]() d﹣17=0,解得d1=
d﹣17=0,解得d1=![]() ,d2=
,d2=![]() ,
,
当∠NMD′=90°时,MD′2=ND′2+MN2,即![]() +d2=d2+
+d2=d2+![]() d+
d+![]() +
+![]() ,
,
化简,得![]() d=﹣
d=﹣![]() ,解得d=﹣
,解得d=﹣![]() ,
,
当∠NMD′﹣90°时,ND′2=MD′2+MN2, ![]() 即d2+
即d2+![]() d+
d+![]() =
=![]() +d2+
+d2+![]() ,
,
化简,得![]() d=
d=![]() ,解得d=
,解得d=![]() ,
,
∴存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1, ![]() )(﹣1,
)(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() )(﹣1
)(﹣1![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级同学到距离学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往目的地。如图,
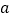 ,
, 分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )
分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )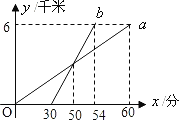
A. 骑车的同学比步行的同学晚出发30分钟 B. 步行的速度是6千米/小时
C. 骑车同学从出发到追上步行同学用了20分钟 D. 骑车同学和步行的同学同时到达目的地
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
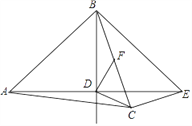
(1)若BD=DE=
 ,CE=
,CE=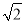 ,求BC的长;
,求BC的长; (2)若BD=DE,求证:BF=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了有理数的加减法之后,老师讲解了例题
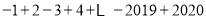 的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.根据这个思路学生改编了下列几题:
(1)计算:①

②

(2)蚂蚁在数轴的原点
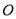 处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……①按照这个规律,第1024次爬行后蚂蚁所在位置在原点左侧还是右侧?对应哪个数?
②按照这个规律,第 次爬行后蚂蚁在数轴上表示751的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方错误的是( )
A. x2+2x﹣99=0化为(x+1)2=100
B. 2x2﹣7x﹣4=0化为
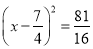
C. x2+8x+9=0化为(x+4)2=25
D. 3x2﹣4x﹣2=0化为(x-
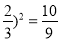
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=4,BC=12,点E是BC的中点.点P、Q分别是边AD、BC上的两点,其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A,同时点Q以每秒2个单位长度的速度从点C出发向点B运动.当其中一点到达终点时停止运动.当运动时间t为_____秒时,以点A、P,Q,E为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的和距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,建立适当坐标系.
(1)求抛物线的解析式.
(2)求两盏景观灯之间的水平距离.

相关试题

