【题目】在![]() ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
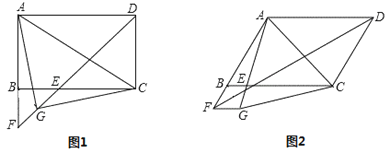
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,判断△AGC的形状.(直接写出结论不必证明)
参考答案:
【答案】(1)①证明见解析;②△AGC是等腰直角三角形.证明见解析;(2)△AGC是等边三角形.
【解析】试题分析:(1)①先判定四边形ABCD是矩形,再根据矩形的性质可得∠ABC=90°,AB∥DC,AD∥BC,然后根据平行线的性质求出∠F=∠FDC,∠BEF=∠ADF,再根据DF是∠ADC的平分线,利用角平分线的定义得到∠ADF=∠FDC,从而得到∠F=∠BEF,然后根据等角对等边的性质即可证明;
②连接BG,根据等腰直角三角形的性质可得∠F=∠BEF=45°,再根据等腰三角形三线合一的性质求出BG=FG,∠F=∠CBG=45°,然后利用“边角边”证明△AFG和△CBG全等,根据全等三角形对应边相等可得AG=CG,再求出∠GAC+∠ACG=90°,然后求出∠AGC=90°,然后根据等腰直角三角形的定义判断即可;
(2)连接BG,根据旋转的性质可得△BFG是等边三角形,再根据角平分线的定义以及平行线的性质求出AF=AD,平行四边形的对角相等求出∠ABC=∠ADC=60°,然后求出∠CBG=60°,从而得到∠AFG=∠CBG,然后利用“边角边”证明△AFG和△CBG全等,根据全等三角形对应边相等可得AG=CG,全等三角形对应角相等可得∠FAG=∠BCG,然后求出∠GAC+∠ACG=120°,再求出∠AGC=60°,然后根据等边三角形的判定方法判定即可.
试题解析:(1)证明:①∵四边形ABCD是平行四边形,∠ADC=90°,
∴四边形ABCD是矩形,∴∠ABC=90°,AB∥DC,AD∥BC,
∴∠F=∠FDC,∠BEF=∠ADF,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,∴∠F=∠BEF,
∴BF=BE;
②△AGC是等腰直角三角形.
理由如下:连接BG,
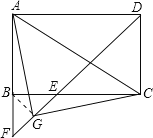
由①知,BF=BE,∠FBC=90°,∴∠F=∠BEF=45°,
∵G是EF的中点,∴BG=FG,∠F=∠CBG=45°,
∵∠FAD=90°,∴AF=AD,又∵AD=BC,∴AF=BC,
在△AFG和△CBG中, 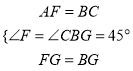 ∴△AFG≌△CBG,
∴△AFG≌△CBG,
∴AG=CG,∠FAG=∠BCG,
又∵∠FAG+∠GAC+∠ACB=90°,∴∠BCG+∠GAC+∠ACB=90°,
即∠GAC+∠ACG=90°,∴∠AGC=90°,∴△AGC是等腰直角三角形;
(2)△AGC是等边三角形.
证明:连接BG,∵FB绕点F顺时针旋转60°至FG,
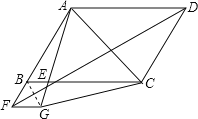
∴△BFG是等边三角形,
∴FG=BG,∠FBG=60°,
又∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠ABC=∠ADC=60°
∴∠CBG=180°-∠FBG-∠ABC=180°-60°-60°=60°,
∴∠AFG=∠CBG,
∵DF是∠ADC的平分线,
∴∠ADF=∠FDC,
∵AB∥DC,
∴∠AFD=∠FDC,
∴∠AFD=∠ADF,
∴AF=AD,
在△AFG和△CBG中,
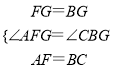 ,
,
∴△AFG≌△CBG(SAS),
∴AG=CG,∠FAG=∠BCG,
在△ABC中,∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°-60°=120°,
∴∠AGC=180°-(∠GAC+∠ACG)=180°-120°=60°,
∴△AGC是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A和B两点在线段EF的中垂线上,且∠EBF=100°,∠EAF=70°,则∠AEB等于( )
A.95°
B.15°
C.95°或15°
D.170°或30° -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程2x2﹣ax+a﹣2=0有两个相等的实根,则a的值是( )
A.﹣4
B.4
C.4或﹣4
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是方程x2﹣x﹣2=0的两个实数根,则代数式2a3+b2+3a2﹣9a﹣b﹣1的值为__.
-
科目: 来源: 题型:
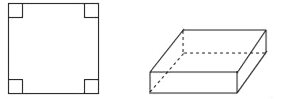
查看答案和解析>>【题目】有一张边长为a厘米的大的正方形纸片,在它的四个角上各减去一个边长为x厘米的小正方形,折成一个无盖的长方体(如图).
(1)当a=9厘米时,请用含x的式子表示这个无盖长方体的体积.
(2)在(1)的条件下,当x=3厘米时求无盖长方体的体积;
(3)当a=12厘米时,要将这张正方形纸片折成一个无盖的正方体,求此时正方体的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3
B.∠1=∠2
C.∠2=∠3
D.∠1=∠2=∠3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有( )
A.1个B.2个C.3个D.4个
相关试题

