【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P. 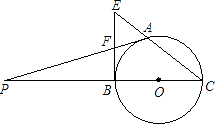
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
参考答案:
【答案】
(1)证明:连接AB,OA,OF;
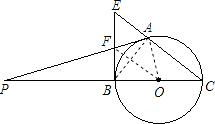
∵F是BE的中点,
∴FE=BF.
∵OB=OC,
∴OF∥EC.
∴∠C=∠POF.
∴∠AOF=∠CAO.
∵∠C=∠CAO,
∴∠POF=∠AOF.
∵BO=AO,OF=OF,
∴∠OAP=∠EBC=90°.
∴PA是⊙O的切线
(2)解:∵BE是⊙O的切线,PA是⊙O的切线,
∴BF=AF=3,
∴BE=6.
∵BC=8,∠CBE=90°,
∴CE=10.
∵BE是⊙O的切线,
∴EB2=AEEC.
∴AE=3.6.
【解析】(1)要想证PA是⊙O的切线,只要连接OA,求证∠OAP=90°即可;(2)先由切线长定理可知BF=AF,再在RT△BCE中根据勾股定理求出CE,最后由切割线定理求出AE的长.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】回答问题:
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=
 ∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=
∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD= ∠AOC,如图1和图2所示,求∠COD的度数.
∠AOC,如图1和图2所示,求∠COD的度数.(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=
 CB,点D是直线AB上满足BD=
CB,点D是直线AB上满足BD= AC.请画出示意图,求出线段CD的长.
AC.请画出示意图,求出线段CD的长.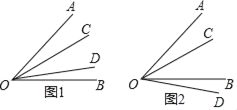
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明身高为1.6米,通过地面上的一块平面镜C,刚好能看到前方大树的树梢E,此时他测得俯角为45度,然后他直接抬头观察树梢E,测得仰角为30度.求树的高度.(结果保留根号)
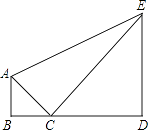
-
科目: 来源: 题型:
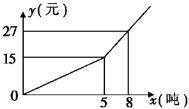
查看答案和解析>>【题目】某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,
(1)分别写出x≤5和x>5的函数解析式;
(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;
(3)若某户居民六月交水费31元,则用水多少吨?
-
科目: 来源: 题型:
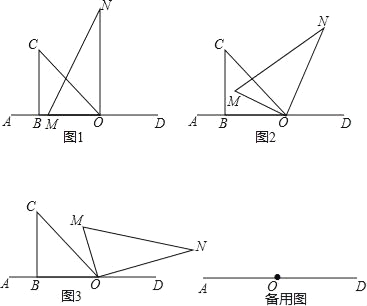
查看答案和解析>>【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
相关试题

