【题目】回答问题:
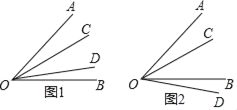
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=![]() ∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=
∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=![]() ∠AOC,如图1和图2所示,求∠COD的度数.
∠AOC,如图1和图2所示,求∠COD的度数.
(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=![]() CB,点D是直线AB上满足BD=
CB,点D是直线AB上满足BD=![]() AC.请画出示意图,求出线段CD的长.
AC.请画出示意图,求出线段CD的长.
参考答案:
【答案】(1) ∠COD的度数为27°或45°,(2)线段CD的长是6cm或10cm
【解析】
(1)分两种情况讨论:①当OD在∠COB内时,②当OD在∠COB外时.根据角的倍分关系先求出∠AOC、∠COB的度数,进一步得到∠BOD的度数,再根据角的和差关系可求∠COD的度数.
(2)分两种情况讨论:①当D在线段CB上时,②当D在线段CB的延长线时.由AB的长,即AC为BC的一半求出AC与BC的长,再由BD为AC一半求出BD的长,由BC﹣BD及BD+BC即可求出CD的长.
(1)分两种情况讨论:①当OD在∠COB内时,如图1.
∵∠AOB的度数为54°,∠AOC=![]() ∠COB,∴∠AOC=18°,∠COB=36°.
∠COB,∴∠AOC=18°,∠COB=36°.
∵∠BOD=![]() ∠AOC,∴∠BOD=9°,∴∠COD=36°-9°=27°;
∠AOC,∴∠BOD=9°,∴∠COD=36°-9°=27°;
②当OD在∠COB外时,如图2.
∵∠AOB的度数为54°,∠AOC=![]() ∠COB,∴∠AOC=18°,∠COB=36°.
∠COB,∴∠AOC=18°,∠COB=36°.
∵∠BOD=![]() ∠AOC,∴∠BOD=9°,∴∠COD=36°+9°=45°;
∠AOC,∴∠BOD=9°,∴∠COD=36°+9°=45°;
综上所述:∠COD的度数为27°或45°.
(2))由题意得:AC=4cm,BC=8cm,BD=2cm.分两种情况讨论:
①当D在线段CB上时,如图1,则CD=BC﹣BD=6(cm);
②当D在线段CB的延长线时,如图2,则CD=BC+BD=10(cm).
综上所述:线段CD的长是6cm或10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有 .
①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0.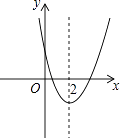
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P.
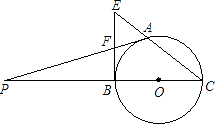
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明身高为1.6米,通过地面上的一块平面镜C,刚好能看到前方大树的树梢E,此时他测得俯角为45度,然后他直接抬头观察树梢E,测得仰角为30度.求树的高度.(结果保留根号)
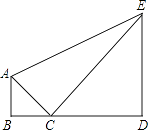
-
科目: 来源: 题型:
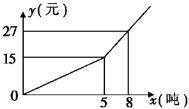
查看答案和解析>>【题目】某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,
(1)分别写出x≤5和x>5的函数解析式;
(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;
(3)若某户居民六月交水费31元,则用水多少吨?
相关试题

