【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=![]() ,AD=1.
,AD=1.

(1)求BC的长;
(2)求tan ∠DAE的值.
参考答案:
【答案】(1)BC= 2![]() +1;(2)tan ∠DAE=
+1;(2)tan ∠DAE=![]() -
-![]() .
.
【解析】试题分析:(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=2![]() ,然后根据BC=BD+DC即可求解;
,然后根据BC=BD+DC即可求解;
(2)先由三角形的中线的定义求出CE的值,则DE=CE-CD,然后在Rt△ADE中根据正切函数的定义即可求解.
试题解析:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=![]() ,AD=1,
,AD=1,
∴AB=![]() =3,
=3,
∴BD=![]() ,
,
∴BC=BD+DC=2![]() +1;
+1;
(2)∵AE是BC边上的中线,
∴CE=![]() BC=
BC=![]() +
+![]() ,
,
∴DE=CE-CD=![]() -
-![]() ,
,
∴tan∠DAE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,
中, ,求证:
,求证: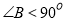 ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:①∴
 ,这与三角形内角和为
,这与三角形内角和为 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴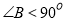 ,③假设在
,③假设在 中,
中, ,④由
,④由 ,得
,得 ,即
,即 .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )A.③④②①B.③④①②C.①②③④D.④③①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t(分钟)的变化规律有如下关系式:
 (y值越大表示接受能力越强)
(y值越大表示接受能力越强)(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中;
(2)讲课开始后多少分钟,学生的注意力最集中能持续多少分钟;
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
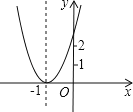
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图,如图所示:


(1)补全条形统计图;
(2)求扇形统计图中扇形D的圆心角的度数;
(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5 h内完成家庭作业.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校对某班学生“五一”小长假期间的度假情况进行调查,并根据收集的数据绘制了两幅不完整的统计图,请你根据图中提供的信息解答下面的问题:

(1)求出该班学生的总人数;
(2)补全频数分布直方图;
(3)求出扇形统计图中∠α的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD的对角线AC、BD交于点O,AE平分BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①AE=CE;②S△ABC=ABAC;③S△ABE=2S△AOE;④OE=
BC,连接OE.下列结论:①AE=CE;②S△ABC=ABAC;③S△ABE=2S△AOE;④OE= BC,成立的个数有( )
BC,成立的个数有( )
A.1个B.2个C.3个D.4
相关试题

