【题目】心理学家研究发现,一般情况下,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t(分钟)的变化规律有如下关系式:  (y值越大表示接受能力越强)
(y值越大表示接受能力越强)
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中;
(2)讲课开始后多少分钟,学生的注意力最集中能持续多少分钟;
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
参考答案:
【答案】(1)讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中;(2)讲课开始后10分钟时,学生的注意力最集中,能持续10分钟;(3)老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目.
【解析】试题分析:
(1)把t=5和t=25分别代入对应的函数关系式求出y的值,并比较大小即可得出结论;
(2)由自变量的取值范围分别求出第一段函数和第三段函数中函数值取最大值时对应的自变量取值结合两段函数的增减性及第二段函数的函数值为固定的240分析即可得到本题答案;
(3)分别在第一段函数和第三段函数中,由y=180解得对应的x的值,即可求得注意力y不低于180的持续时间是多长,由此即可得到本题答案.
试题解析:
(1)当t=5时,y=195,当t=25时,y=205
∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中.
(2)①当0<t≤10时,y=﹣t2+24t+100=﹣(t﹣12)2+244,
该段函数图象的对称轴为直线t=12,在对称轴左侧,y随x的增大而增大,
∴当t=10时,y有最大值240;
②当10<t≤20时,y=240;
③当20<t≤40时,y=﹣7t+380,y随t的增大而减小,
故此时y<240;
∴综上所述,当t=10时,y有最大值240,持续时间为:20-10=10(分钟),
即:讲课开始后10分钟时,学生的注意力最集中,能持续10分钟.
(3)当0<t≤10,令y=﹣t2+24t+100=180,解得t1=4,t2=20(不在取值范围内,舍去),
当20<t≤40时,令y=﹣7t+380=180,解得t=28.57
∵28.57﹣4>24,
∴老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数
 的图象于B点,交函数
的图象于B点,交函数 的图象于C,过C作y轴和平行线交BO的延长线于D.
的图象于C,过C作y轴和平行线交BO的延长线于D.(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比;
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比;
(3)在(1)条件下,四边形AODC的面积为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,
中, ,求证:
,求证: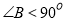 ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:①∴
 ,这与三角形内角和为
,这与三角形内角和为 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴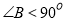 ,③假设在
,③假设在 中,
中, ,④由
,④由 ,得
,得 ,即
,即 .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )A.③④②①B.③④①②C.①②③④D.④③①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
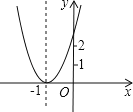
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=
 ,AD=1.
,AD=1.
(1)求BC的长;
(2)求tan ∠DAE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图,如图所示:


(1)补全条形统计图;
(2)求扇形统计图中扇形D的圆心角的度数;
(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5 h内完成家庭作业.
相关试题

