【题目】定义:如果三角形有一边上的中线长恰好等于这边的长,那么这个三角形叫“恰等三角形”,这条中线叫“恰等中线”.
(直角三角形中的“恰等中线”)
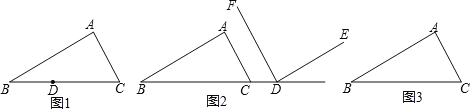
(1)如图1,在△ABC中,∠C=90°,AC=![]() ,BC=2,AM为△ABC的中线.求证:AM是“恰等中线”.
,BC=2,AM为△ABC的中线.求证:AM是“恰等中线”.

(等腰三角形中的“恰等中线”)
(2)已知,等腰△ABC是“恰等三角形”,AB=AC=20,求底边BC的平方.
(一般三角形中的“恰等中线”)
(3)如图2,若AM是△ABC的“恰等中线”,则BC2,AB2,AC2之间的数量关系为 .

参考答案:
【答案】(1)见详解;(2)600或320;(3)![]() .
.
【解析】
(1)根据“恰等中线”的定义和勾股定理,判定即可;
(2)利用“恰等三角形”的定义,分类讨论:①若腰上的中线为“恰等中线”,过B作腰AC边上的高,利用勾股定理即可求出BC2;②若底的中线为“恰等中线”,利用勾股定理求BC2即可;
(3)过A作AD⊥BC,交BC于点D,再利用勾股定理列等式即可.
解:(1)∵BC=2,AM为△ABC的中线

∴CM=![]()
在Rt△AMC中,
AM=![]() ,
,
∴AM=BC
∴AM是“恰等中线”.
(2)①若腰上的中线为“恰等中线”,假设BD是“恰等中线”,过B作BN⊥AC,如图所示:

∵AB=AC=20,BD是AC的“恰等中线”
∴BD=AC=20,AD=DC=10
∴△ABD为等腰三角形,
∵BN⊥AC
∴AN=DN=![]()
∴![]()
NC=ND+DC=15
∴![]()
②若底的中线为“恰等中线”,如下图所示AD为“恰等中线”,设

∴AD=BC,且BD=CD=![]()
∵AB=AC=20
∴AD⊥BC
在Rt△ABD中

解得:![]()
综上所述:![]() 或320.
或320.
(3)过点A作AD⊥BC交BC于D,

∵AM是△ABC的“恰等中线”
∴AM=BC,BM=CM=![]()
在Rt△ABD,Rt△AMD和Rt△ACD中
![]() ,
,![]() ,
,![]()
∴  ,
,
由①②变形得:

将③+④得:![]()
=![]()
=![]()
将AM=BC,BM=CM=![]() 代入得:
代入得:
![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC.
(2)若PB=5,PH=3,求AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC和同一平面内的点D.
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
①依题意,在图1中补全图形;
②判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,若点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,自己在草稿纸上试着画一画,看一看会有几种情况,然后直接写出∠EDF与∠A的数量关系(不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3b|+(a+b-4)=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若
 ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:(1)试说明
 ;
;(2)如果大正方形的面积是10,小正方形的面积是2,求
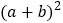 的值.
的值.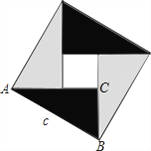
相关试题

