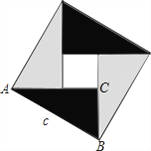
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.
参考答案:
【答案】见解析
【解析】试题分析:(1)根据大正方形面积=小正方形面积+4个直角三角形面积计算即可;
(2)由图可得到(b-a)2和2ab的值,代入(a+b)2=(b-a)2+4ab,即可得到结论.
试题解析:解:(1)∵大正方形面积为c2,直角三角形面积为![]() ab,小正方形面积为(b-a)2,∴c2=4×
ab,小正方形面积为(b-a)2,∴c2=4×![]() ab+(a-b)2=2ab+a2-2ab+b2 即c2=a2+b2;
ab+(a-b)2=2ab+a2-2ab+b2 即c2=a2+b2;
(2) 由图可知,(b-a)2=2, 4×![]() ab=10-2=8, ∴2ab=8,(a+b)2=(b-a)2+4ab=2+2×8=18.
ab=10-2=8, ∴2ab=8,(a+b)2=(b-a)2+4ab=2+2×8=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:已知
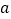 、
、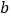 、
、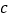 为△ABC的三边,且满足
为△ABC的三边,且满足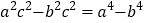 ,
,试判断△ABC的形状.
解:∵
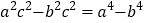 ①
① ∴
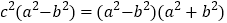 ②
②∴
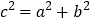 ③
③∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的重量(kg)之间的关系如下表:
所挂物体的重量(kg)
0
1
2
3
4
5
6
7
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
15
15.5
(1)当所挂物体的重量为3kg时,弹簧的长度是_____________cm;
(2)如果所挂物体的重量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的重量为5.5kg时,请求出弹簧的长度。
(4)如果弹簧的最大伸长长度为20cm,则该弹簧最多能挂多重的物体?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向
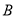 点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻
点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻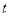 ,使以A,M,N为顶点的三角形与△ACD相似?若存在,求
,使以A,M,N为顶点的三角形与△ACD相似?若存在,求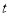 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.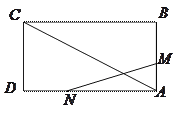
-
科目: 来源: 题型:
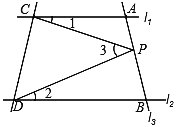
查看答案和解析>>【题目】如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.
(1)试说明∠1,∠2,∠3之间的关系式;(要求写出推理过程)
(2)如果点P在A、B两点之间(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系是否发生变化?(只回答)
(3)如果点P在A、B两点外侧(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系.(要求写出推理过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的正方形网格(每个小正方形的边长均为1)中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴(水平线为横轴),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称.

(1)原点是 (填字母A,B,C,D );
(2)若点P在3×3的正方形网格内的坐标轴上,且与四个格点A,B,C,D,中的两点能构成面积为1的等腰直角三角形,则点P的坐标为 (写出可能的所有点P的坐标)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用的练习本可以到甲超市购买,也可以到乙超市购买.已知两超市的标价都是每本1元,但甲超市的优惠条件是购买10本以上,从第11本开始按标价的70%卖.乙超市的优惠条件是从第1本开始就按标价的85%卖.
(1)当小明要买20本时,到哪家超市购买较省钱?
(2)写出甲超市中,收款y甲(元)与购买本数x(本)(x>10)的关系式.
(3)小明现有24元钱,最多可买多少本练习本?
相关试题

