搜索
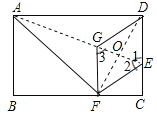
【题目】如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作FG∥CD，交AE于点G，连接DG．
（1）求证：四边形DEFG为菱形；
（2）若CD=8，CF=4，求
的值．
参考答案：
【答案】（1）证明见试题解析；（2）
．
【解析】试题分析：（1）由折叠的性质，可以得到DG=FG，ED=EF，∠1=∠2，由FG∥CD，可得∠1=∠3，再证明 FG=FE，即可得到四边形DEFG为菱形；
（2）在Rt△EFC中，用勾股定理列方程即可CD、CE，从而求出
的值．
试题解析：（1）由折叠的性质可知：DG=FG，ED=EF，∠1=∠2，∵FG∥CD，∴∠2=∠3，∴FG=FE，∴DG=GF=EF=DE，∴四边形DEFG为菱形；
（2）设DE=x，根据折叠的性质，EF=DE=x，EC=8﹣x，在Rt△EFC中，
，即
，解得：x=5，CE=8﹣x=3，∴=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，下列条件中，不能使四边形DBCE成为菱形的是（ ）
A.AB＝BEB.BE⊥DCC.∠ABE＝90°D.BE平分∠DBC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A、B两点的坐标分别为（40，0）和（0，30），动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每秒1个单位的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．
（1）求t=15时，△PEF的面积；
（2）直线EF、点P在运动过程中，是否存在这样的t，使得△PEF的面积等于160（平方单位）？若存在，请求出此时t的值；若不存在，请说明理由．
（3）当t为何值时，△EOP与△BOA相似．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD＝2BC，∠ABD＝90°，E为AD的中点，连接BE．
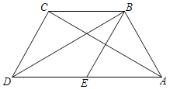
（1）求证：四边形BCDE为菱形；
（2）连接AC，若AC平分∠BAD，AB＝2，求菱形BCDE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2019年4月23日是第24个世界读书日．为了弘扬中华传统文化，我县某学校举办了“让读书成为习惯，让书香飘满校园”主题活动，为此特为每个班级订购了一批新的图书．初一(1)班订购老舍文集4套和四大名著2套，总费用为480元；初一(2)班订购老舍文集2套和四大名著3套，总费用为520元．
(1)求老舍文集和四大名著每套各是多少元？
(2)学校准备再购买老舍文集和四大名著共20套，总费用不超过1720元，购买老舍文集的数量不超过四大名著的3倍，问学校有几种购买方案，请你设计出来．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）在Rt△ABC中，∠BAC=
,D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F．
（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=4，AB=5，求菱形ADCFD 的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．
（1）求证：ABCD是菱形；
（2）若AB=5，AC=6，求ABCD的面积．
相关试题
