Question

【题目】已知：△ABC和同一平面内的点D．

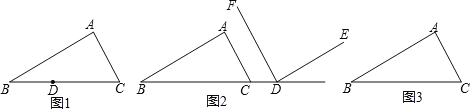
（1）如图1，点D在BC边上，过D作DE∥BA交AC于E，DF∥CA交AB于F．

①依题意，在图1中补全图形；

②判断∠EDF与∠A的数量关系，并直接写出结论(不需证明)．

（2）如图2，点D在BC的延长线上，DF∥CA，∠EDF=∠A．判断DE与BA的位置关系，并证明．

（3）如图3，若点D是△ABC外部的一个动点，过D作DE∥BA交直线AC于E，DF∥CA交直线AB于F，自己在草稿纸上试着画一画，看一看会有几种情况，然后直接写出∠EDF与∠A的数量关系(不需证明)．

Answer 1

【答案】（1）①作图见解析；②∠EDF=∠A；（2）DE∥BA，证明见解析；（3）∠EDF=∠A，∠EDF+∠A=180°．

【解析】

（1）根据过D作DE∥BA交AC于E，DF∥CA交AB于F，进行作图；根据平行线的性质，即可得到∠A=∠EDF；

（2）延长BA交DF于G．根据平行线的性质以及判定进行推导即可；

（3）分两种情况讨论，即可得到∠EDF与∠A的数量关系：∠EDF=∠A，∠EDF+∠A=180°．

（1）①补全图形如图1；

②∠EDF=∠A．

理由：∵DE∥BA，DF∥CA，∴∠A=∠DEC，∠DEC=∠EDF，∴∠A=∠EDF；

（2）DE∥BA．

证明：如图，延长BA交DF于G．

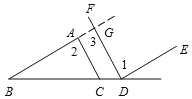
∵DF∥CA，∴∠2=∠3．

又∵∠1=∠2，∴∠1=∠3，∴DE∥BA．

（3）∠EDF=∠A，∠EDF+∠A=180°．

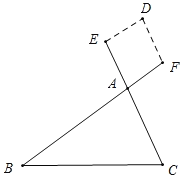
理由：如左图．

∵DE∥BA，DF∥CA，∴∠D+∠E=180°，∠E+∠EAF=180°，∴∠EDF=∠EAF=∠BAC；

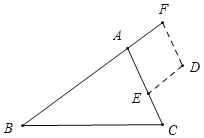
如右图．

∵DE∥BA，DF∥CA，∴∠D+∠F=180°，∠F=∠CAB，∴∠EDF+∠BAC=180°．