【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.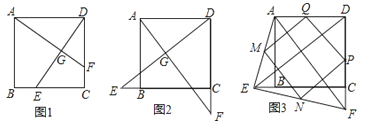
参考答案:
【答案】解:(1)上述结论①,②仍然成立,
理由为:∵四边形ABCD为正方形,
∴AD=DC,∠BCD=∠ADC=90°,
在△ADF和△DCE中,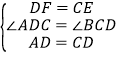 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠ADG+∠EDC=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,即AF⊥DE;
(2)上述结论①,②仍然成立,
理由为:∵四边形ABCD为正方形,
∴AD=DC,∠BCD=∠ADC=90°,
在△ADF和△DCE中,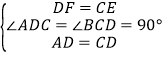 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠CDE=∠DAF,
∵∠ADG+∠EDC=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,即AF⊥DE;
(3)四边形MNPQ是正方形.
理由为:如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,
∵点M,N,P,Q分别为AE,EF,FD,AD的中点,
∴MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,
AF,MQ∥DE,PQ∥AF,
∴四边形OHQG是平行四边形,
∵AF=DE,
∴MQ=PQ=PN=MN,
∴四边形MNPQ是菱形,
∵AF⊥DE,
∴∠AOD=90°,
∴∠HQG=∠AOD=90°,
∴四边形MNPQ是正方形.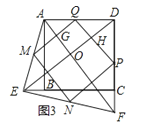
【解析】(1)由四边形ABCD为正方形,CE=DF,易证得△ADF≌△DCE(SAS),即可证得AF=DE,∠DAF=∠CDE,又由∠ADG+∠EDC=90°,即可证得AF⊥DE;
(2)由四边形ABCD为正方形,CE=DF,易证得△ADF≌△DCE(SAS),即可证得AF=DE,∠E=∠F,又由∠ADG+∠EDC=90°,即可证得AF⊥DE;
(3)首先设MQ,DE分别交AF于点G,O,PQ交DE于点H,由点M,N,P,Q分别为AE,EF,FD,AD的中点,即可得MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,然后由AF=DE,可证得四边形MNPQ是菱形,又由AF⊥DE即可证得四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,然后由AF=DE,可证得四边形MNPQ是菱形,又由AF⊥DE即可证得四边形MNPQ是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式的一次项系数是﹣5,二次项系数是8,常数项是﹣2,且只含一个字母x,请写出这个多项式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
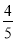 ,反比例函数
,反比例函数 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
A. 10 B. 9 C. 8 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值
(1)3(x﹣3y)﹣2(y﹣2x)﹣x.
(2)已知:A=m2﹣2n2+2m,B=2m2﹣3n2﹣m,求B﹣2A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:
(1)这个班有多少人参加了本次数学调研考试?
(2)60.5~70.5分数段的频数和频率各是多少?
(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.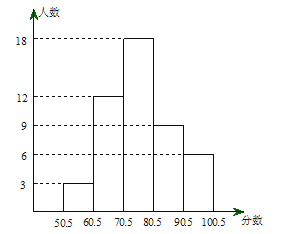
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;②
 ;③
;③ =Ac·AD;④OE:OA=1:
=Ac·AD;④OE:OA=1:  其中结论正确的序号是____.(把所有正确结论的序号都选上)
其中结论正确的序号是____.(把所有正确结论的序号都选上)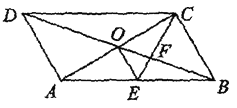
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与b互为倒数,c与d互为相反数,x的绝对值是3,求2(ab)2016+c+d+2x的值.
相关试题

