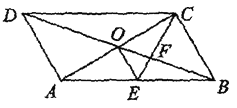
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;②![]() ;③
;③![]() =Ac·AD;④OE:OA=1:
=Ac·AD;④OE:OA=1: ![]() 其中结论正确的序号是____.(把所有正确结论的序号都选上)
其中结论正确的序号是____.(把所有正确结论的序号都选上)
参考答案:
【答案】①③④
【解析】∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
②![]() 不正确,
不正确,
∵AC⊥BC,
∴![]() =Ac·AD,故③正确,
=Ac·AD,故③正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=![]() BC,
BC,
∵AO=OC,AE=BE,
∴OE=![]() BC,OA=
BC,OA=![]() BC,
BC,
∴OE:OA= =
=![]() ,
,
故④正确;
答案为:①③④
“点睛”此题考查了相似三角形的判定和性质,平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△BCE是等边三角形,OE是△ABC的中位线是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值
(1)3(x﹣3y)﹣2(y﹣2x)﹣x.
(2)已知:A=m2﹣2n2+2m,B=2m2﹣3n2﹣m,求B﹣2A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.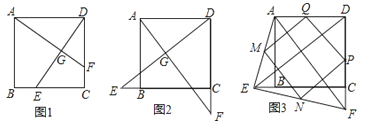
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:
(1)这个班有多少人参加了本次数学调研考试?
(2)60.5~70.5分数段的频数和频率各是多少?
(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.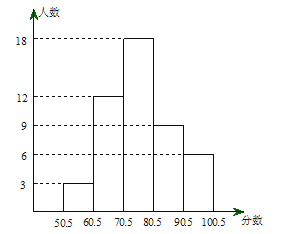
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与b互为倒数,c与d互为相反数,x的绝对值是3,求2(ab)2016+c+d+2x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A. a4+a4=a8B. a3a2=a5C. a8÷a2=a4D. (-2a2)3=-6a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=( )
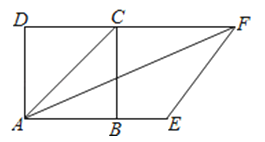
A.30°
B.45°
C.22.5°
D.135°
相关试题

