搜索
【题目】如图，AE、BO、CO分别平分∠BAC、∠ABC、∠ACB，OD⊥BC，试说明：∠1=∠2.
参考答案：
【答案】见解析.
【解析】根据角平分线的定义和三角形的一个外角等于和它不相邻的两个内角的和，∠1等于∠ABC与∠BAC的一半的和，∠2等于90°减去∠ACB的一半，而∠ABC、∠ACB、∠BAC三个角的一半等于90°，所以∠2等于∠ABC与∠BAC的一半的和，所以∠1与∠2相等．
∵AE、B0、CO分别平分∠BAC、∠ABC、∠ACB,
∴∠AB0=
∠ABC,∠BAE=∠BAC,
∠OCD=∠ACB.
∵∠1=∠ABO+∠BAE=∠ABC+∠BAC=(180°-∠ACB)=90°-∠ACB，
而∠2=90°-∠ACB，
∴∠1=∠2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校260名学生参加植树活动，要求每人植4﹣7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵，将各类的人数绘制成扇形图（如图（1））和条形图（如图（2）），经确认扇形图是正确的，而条形图尚有一处错误． 回答下列问题：
（1）写出条形图中存在的错误，并说明理由；
（2）写出这20名学生每人植树量的众数、中位数；
（3）在求这20名学生每人植树量的平均数时，小宇是这样分析的： 第一步：求平均数的公式是
= 
；
第二步：在该问题中，n=4，x1=4，x2=5，x3=6，x4=7；
第三步：
= 
=5.5（份）
①小宇的分析是从哪一步开始出现错误的？
②请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵． -
科目： 来源： 题型：
查看答案和解析>>【题目】根据条件画图，并回答问题：
(1)画一个锐角△ABC(三边均不相等)；
(2)画出BC边上的中线AE和高AD；
(3)写出所有以AD为高的三角形。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O半径为4cm，其内接正六边形ABCDEF，点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向中点F，G运动．连接PB，QE，设运动时间为t（s）．
（1）求证：四边形PEQB为平行四边形；
（2）填空： ①当t=s时，四边形PBQE为菱形；
②当t=s时，四边形PBQE为矩形． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，商丘市睢阳区南湖中有一小岛，湖边有一条笔直的观光小道，现决定从小岛架一座与观光小道垂直的小桥PD，小坤在小道上测得如下数据：AB=200.0米，∠PAB=38.5°，∠PBA=26.5°．请帮助小坤求出小桥PD的长．（结果精确到0.1米） （参考数据：sin38.5°≈0.62，cos38.5°≈0.78，tan38.5°≈0.80，sin26.5°≈0.45，cos26.5°≈0.89，tan26.5°≈0.50）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，线段AB、CD相交于点O，连结AD、CB，我们把这个图形称为“8字型”根据三角形内角和容易得到：∠A+∠D=∠C+∠B.
(1)用“8字型”
如图2,∠A+∠B+∠C+∠D+∠E+∠F=___________；
(2)造“8字型”
如图3,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_____________;
(3)发现“8字型”
如图4，BE、CD相交于点A，CF为∠BCD的平分
线，EF为∠BED的平分线.
①图中共有________个“8字型”；
②若∠B：∠D：∠F=4：6：x，求x的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】重阳节期间，某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游，由于人数较多，共租用甲、乙两辆长途汽车沿同一路线赶赴景点．图中的折线、线段分别表示甲、乙两车所走的路程y甲（千米），y乙（千米）与时间x（小时）之间的函数关系对应的图象．请根据图象所提供的信息，解决下列问题：
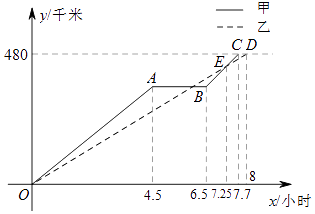
（1）由于汽车发生故障，甲车在途中停留了小时；
（2）甲车排除故障后，立即提速赶往景点．请问甲车在排除故障时，距出发点的路程是多少千米？
（3）为了保证及时联络，甲、乙车在第一次相遇时约定此后两车之间的路程不超过35千米，请通过计算说明，按图象所表示的走法是否符合约定．
相关试题
