【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把这个图形称为“8字型”根据三角形内角和容易得到:∠A+∠D=∠C+∠B.


(1)用“8字型”
如图2,∠A+∠B+∠C+∠D+∠E+∠F=___________;
(2)造“8字型”
如图3,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_____________;
(3)发现“8字型”
如图4,BE、CD相交于点A,CF为∠BCD的平分
线,EF为∠BED的平分线.
①图中共有________个“8字型”;
②若∠B:∠D:∠F=4:6:x,求x的值.
参考答案:
【答案】(1)360°;(2)540;(3)①6;②x=5.
【解析】(1)根据题意即可得到结论;
(3)①由图形即可得到结论;
②根据三角形内角和为180°的性质即可证得关系为∠D+∠B=2∠F,再根据∠B、∠D、∠F的比值,即可求得x的值;
(1)∵∠A+∠B=∠GKH+∠GHK,
∠C+∠D=∠GHK+∠HGK,
∠E+∠F=∠HGK+∠GKH,
∠A+∠B+∠C+∠D+∠E+∠F=2(∠GKH+∠GHK+∠HGK)=2×180°=360°,故答案为:360°;
(2)如图,连结BC,
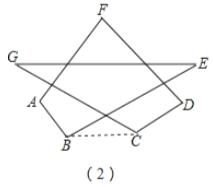
∵∠E+∠G=∠GCB+∠EBC,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=五边形FABCD的内角和,
即∠A+∠B+∠C+∠D+∠E+∠F+∠G=(5-2)180°=540°,
故答案为:540°;
(3)①图中共有6个“8字型”;
故答案为:6.
②:∵CF平分∠BCD,EF平分∠BED
∴∠DEG=∠AEG,∠ACH=∠BCH,
∵在△DGE和△FGC中,∠DGE=∠FGC
∴∠D+∠DEG=∠F+∠ACH
∵在△BHC和△FHE中,∠BHC=∠FHE
∴∠B+∠BCH=∠F+∠AEG
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG
∴∠D+∠B=2∠F;
∵∠B:∠D:∠F=4:6:x,∠D+∠B=2∠F,
∴x=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).

(1)求证:四边形PEQB为平行四边形;
(2)填空: ①当t=s时,四边形PBQE为菱形;
②当t=s时,四边形PBQE为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE、BO、CO分别平分∠BAC、∠ABC、∠ACB,OD⊥BC,试说明:∠1=∠2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米) (参考数据:sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80,sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50)

-
科目: 来源: 题型:
查看答案和解析>>【题目】重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
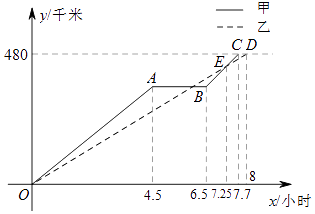
(1)由于汽车发生故障,甲车在途中停留了小时;
(2)甲车排除故障后,立即提速赶往景点.请问甲车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙车在第一次相遇时约定此后两车之间的路程不超过35千米,请通过计算说明,按图象所表示的走法是否符合约定. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
相关试题

