【题目】某高校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．
（1）这次被调查的同学共有名；
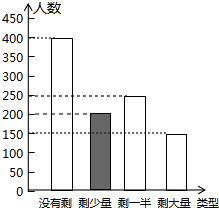
（2）把条形统计图补充完整；
（3）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校18 000名学生一餐浪费的食物可供多少人食用一餐？

参考答案：

【答案】
（1）1000
（2）解：剩少量的人数是；1000﹣400﹣250﹣150=200，

补图如下；


（3）解：18000× =3600（人）．

答：该校18000名学生一餐浪费的食物可供3600人食用一餐


【解析】解：（1）这次被调查的同学共有400÷40%=1000（名）； 故答案为：1000；
（1）用没有剩的人数除以其所占的百分比即可；（2）用抽查的总人数减去其他三类的人数，再画出图形即可；（3）根据这次被调查的所有学生一餐浪费的食物可以供200人用一餐，再根据全校的总人数是18000人，列式计算即可．

关闭