【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( ) 
A.1.8
B.2.4
C.3.2
D.3.6
参考答案:
【答案】D
【解析】解:连接BF, 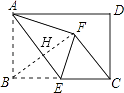
∵BC=6,点E为BC的中点,
∴BE=3,
又∵AB=4,
∴AE= ![]() =5,
=5,
∴BH= ![]() ,
,
则BF= ![]() ,
,
∵FE=BE=EC,
∴∠BFC=90°,
∴CF= ![]() =3.6.
=3.6.
故选:D.
【考点精析】通过灵活运用矩形的性质和翻折变换(折叠问题),掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等腰直角
 放在直角坐标系内,其中
放在直角坐标系内,其中 ,点
,点 、
、 的坐标分别为
的坐标分别为 ,将等腰直角
,将等腰直角 沿
沿 轴向右平移,当点
轴向右平移,当点 落在直线
落在直线 上时,则线段
上时,则线段 扫过的面积为________.
扫过的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知二次函数y=x2+bx+c的图象与x 轴交于A(﹣1,0)、B(3,0)两点,与y 轴交于点C,顶点为D,对称轴为直线l.
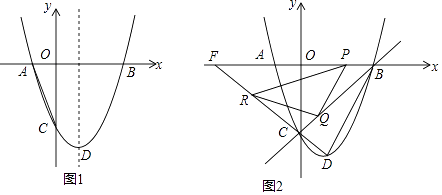
(1)求该二次函数的表达式;
(2)若点E 是对称轴l 右侧抛物线上一点,且S△ADE=2S△AOC , 求点E 的坐标;
(3)如图2,连接DC 并延长交x 轴于点F,设P 为线段BF 上一动点(不与B、F 重合),过点P 作PQ∥BD 交直线BC 于点Q,将直线PQ 绕点P 沿顺时针方向旋转45°后,所得的直线交DF 于点R,连接QR.请直接写出当△PQR 与△PFR 相似时点P 的坐标.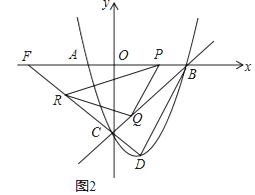
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在矩形
,在矩形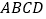 中,
中,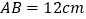 ,
,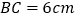 ,点
,点 从
从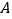 点出发,沿
点出发,沿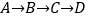 路线运动,到
路线运动,到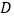 点停止;点
点停止;点 从
从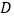 点出发,沿
点出发,沿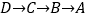 运动,到
运动,到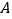 点停止.若点
点停止.若点 、点
、点 同时出发,点
同时出发,点 的速度为每秒
的速度为每秒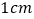 ,点
,点 的速度为每秒
的速度为每秒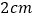 ,
,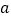 秒时点
秒时点 、点
、点 同时改变速度,点
同时改变速度,点 的速度变为每秒
的速度变为每秒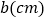 ,点
,点 的速度变为每秒
的速度变为每秒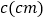 .如图
.如图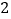 是点
是点 出发
出发 秒后
秒后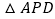 的面积
的面积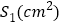 与
与 (秒)的函数关系图象;图
(秒)的函数关系图象;图 是点
是点 出发
出发 秒后
秒后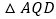 的面积
的面积 与
与 (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象: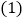 求
求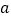 、
、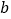 、
、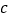 的值;
的值;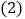 设点
设点 出发
出发 (秒)后离开点
(秒)后离开点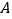 的路程为
的路程为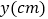 ,请写出
,请写出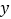 与
与 的函数关系式,并求出点
的函数关系式,并求出点 与
与 相遇时
相遇时 的值.
的值.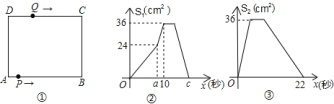
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
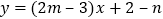 满足下列条件,分别求出
满足下列条件,分别求出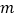 ,
, 的取值范围.
的取值范围.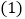 使得
使得 随
随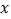 增加而减小.
增加而减小.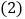 使得函数图象与
使得函数图象与 轴的交点在
轴的交点在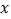 轴的上方.
轴的上方.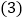 使得函数图象经过一、三、四象限.
使得函数图象经过一、三、四象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是 . (结果保留根号)

-
科目: 来源: 题型:
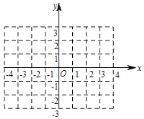
查看答案和解析>>【题目】已知一次函数
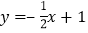 ,它的图象与
,它的图象与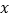 轴交于点
轴交于点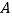 ,与
,与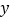 轴交于点
轴交于点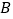 .
.
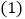 点
点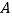 的坐标为________,点
的坐标为________,点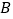 的坐标为________;
的坐标为________; 画出此函数图象;
画出此函数图象; 画出该函数图象向下平移
画出该函数图象向下平移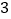 个单位长度后得到的图象;
个单位长度后得到的图象; 写出一次函数
写出一次函数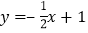 图象向下平移
图象向下平移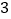 个单位长度后所得图象对应的表达式.
个单位长度后所得图象对应的表达式.
相关试题

