【题目】如图1,已知二次函数y=x2+bx+c的图象与x 轴交于A(﹣1,0)、B(3,0)两点,与y 轴交于点C,顶点为D,对称轴为直线l.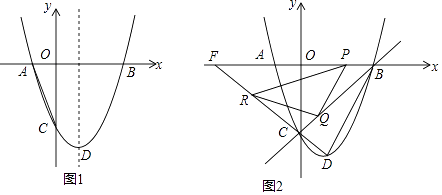
(1)求该二次函数的表达式;
(2)若点E 是对称轴l 右侧抛物线上一点,且S△ADE=2S△AOC , 求点E 的坐标;
(3)如图2,连接DC 并延长交x 轴于点F,设P 为线段BF 上一动点(不与B、F 重合),过点P 作PQ∥BD 交直线BC 于点Q,将直线PQ 绕点P 沿顺时针方向旋转45°后,所得的直线交DF 于点R,连接QR.请直接写出当△PQR 与△PFR 相似时点P 的坐标.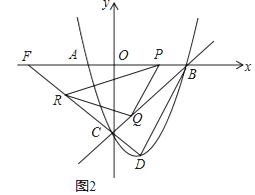
参考答案:
【答案】
(1)
解:将点A和点B的坐标代入抛物线的解析式得 ![]() ,解得
,解得 ![]() ,
,
∴二次函数的表达式为y=x2﹣2x﹣3;
(2)
解:设E(m,m2﹣2m﹣3),过点E作EM∥x轴,交AD于点M,(如图1)
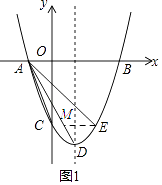
由y=x2﹣2x﹣3=( x﹣1)2﹣4得顶点D(1,﹣4),C(0,﹣3),
∴ ![]() ,
,
∴S△ADE=2S△AOC=3,
∵A(﹣1,0)、D(1,﹣4),
∴直线AD为:y=﹣2x﹣2,
∵E(m,m2﹣2m﹣3),
∴M( ![]() ,m2﹣2m﹣3),
,m2﹣2m﹣3),
∴EM= ![]() ,
,
∴S△ADE ![]() ×4×EM=2EM=m2﹣1=3,
×4×EM=2EM=m2﹣1=3,
解得m=±2(其中m=﹣2舍去),
∴E(2﹣3);
(3)
解:∵C(0,﹣3),D(1,﹣4),
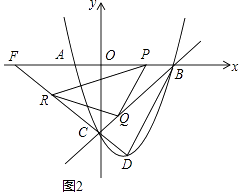
∴直线CD的解析式为:y=﹣x﹣3.
当y=0时,x=﹣3,
故F(0,﹣3),
∴OF=OC=3,
∴∠OFC=45°,即∠PFR=45°.
∵PQ∥BD,
∴∠FPQ≠90°,
∴∠FPR≠45°,
∴当△PQR 与△PFR 相似时:
△PQR∽△FRP,则
点P的坐标是:P1( ![]() ,0)、P2(0,0).
,0)、P2(0,0).
【解析】(1)由A、B两点的坐标,利用待定系数法可求得二次函数的表达式;(2)设E(m,m2﹣2m﹣3),过点E作EM∥x轴,交AD于点M,由条件可得△AOC的面积,从而可求得△ADE的面积,利用待定系数法可求得直线AD的解析式,则可用m表示出EM的长,从而可用m表示出△ADE的面积,从而可得到关于m的方程,可求得m的值;(3)由C、D坐标可求得直线CD的解析式,从而可求得F点坐标,可求得OF=OC,可得∠RFP=∠RPQ=45°,由△PQR 与△PFR 相似得到:△PQR∽△FRP 或△PQR∽△FPR,结合相似三角形的对应边成比例得到点P的坐标.
【考点精析】通过灵活运用确定一次函数的表达式和三角形的面积,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2 台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000 元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请你帮该商场设计一种进货方案,使得在售完这10 台空调后获利最大,并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知直线l1经过原点O 及A(2,2
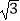 )两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B.
)两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B. 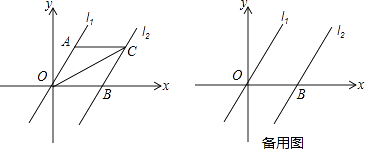
(1)求直线l2的函数表达式;
(2)作∠AOB 的平分线交直线l2于点C,连接AC.求证:四边形OACB是菱形;
(3)设点P 是直线l2上一点,以P 为圆心,PB 为半径作⊙P,当⊙P 与直线l1相切时,请求出圆心P 点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等腰直角
 放在直角坐标系内,其中
放在直角坐标系内,其中 ,点
,点 、
、 的坐标分别为
的坐标分别为 ,将等腰直角
,将等腰直角 沿
沿 轴向右平移,当点
轴向右平移,当点 落在直线
落在直线 上时,则线段
上时,则线段 扫过的面积为________.
扫过的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在矩形
,在矩形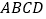 中,
中,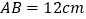 ,
,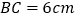 ,点
,点 从
从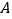 点出发,沿
点出发,沿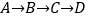 路线运动,到
路线运动,到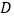 点停止;点
点停止;点 从
从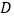 点出发,沿
点出发,沿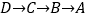 运动,到
运动,到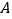 点停止.若点
点停止.若点 、点
、点 同时出发,点
同时出发,点 的速度为每秒
的速度为每秒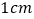 ,点
,点 的速度为每秒
的速度为每秒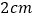 ,
,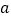 秒时点
秒时点 、点
、点 同时改变速度,点
同时改变速度,点 的速度变为每秒
的速度变为每秒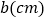 ,点
,点 的速度变为每秒
的速度变为每秒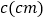 .如图
.如图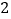 是点
是点 出发
出发 秒后
秒后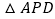 的面积
的面积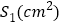 与
与 (秒)的函数关系图象;图
(秒)的函数关系图象;图 是点
是点 出发
出发 秒后
秒后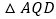 的面积
的面积 与
与 (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象: 求
求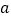 、
、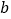 、
、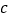 的值;
的值;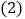 设点
设点 出发
出发 (秒)后离开点
(秒)后离开点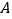 的路程为
的路程为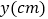 ,请写出
,请写出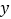 与
与 的函数关系式,并求出点
的函数关系式,并求出点 与
与 相遇时
相遇时 的值.
的值.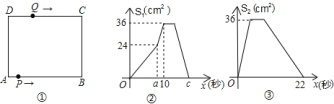
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )

A.1.8
B.2.4
C.3.2
D.3.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
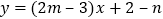 满足下列条件,分别求出
满足下列条件,分别求出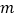 ,
, 的取值范围.
的取值范围.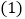 使得
使得 随
随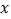 增加而减小.
增加而减小.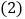 使得函数图象与
使得函数图象与 轴的交点在
轴的交点在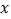 轴的上方.
轴的上方.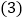 使得函数图象经过一、三、四象限.
使得函数图象经过一、三、四象限.
相关试题

