【题目】如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是 . (结果保留根号) 
参考答案:
【答案】![]()
【解析】解:如图,设BF交CE于点H, 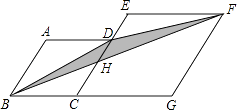
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴ ![]() ,
,
即 ![]() ,
,
解得CH= ![]() ,
,
所以,DH=CD﹣CH=2﹣ ![]() ,
,
∵∠A=120°,
∴∠ECG=∠ABC=180°﹣120°=60°,
∴点B到CD的距离为2× ![]() ,
,
点G到CE的距离为4× ![]() ,
,
∴阴影部分的面积=S△BDH+S△FDH ,
= ![]() ,
,
= ![]() .
.
故答案为: ![]()
设BF交CE于点H,根据菱形的对边平行,利用相似三角形对应边成比例列式求出CH,然后求出DH,根据菱形邻角互补求出∠ABC=60°,再求出点B到CD的距离以及点G到CE的距离;然后根据阴影部分的面积=S△BDH+S△FDH , 根据三角形的面积公式列式进行计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在矩形
,在矩形 中,
中, ,
,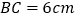 ,点
,点 从
从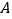 点出发,沿
点出发,沿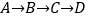 路线运动,到
路线运动,到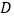 点停止;点
点停止;点 从
从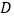 点出发,沿
点出发,沿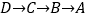 运动,到
运动,到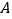 点停止.若点
点停止.若点 、点
、点 同时出发,点
同时出发,点 的速度为每秒
的速度为每秒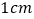 ,点
,点 的速度为每秒
的速度为每秒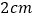 ,
,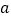 秒时点
秒时点 、点
、点 同时改变速度,点
同时改变速度,点 的速度变为每秒
的速度变为每秒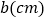 ,点
,点 的速度变为每秒
的速度变为每秒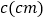 .如图
.如图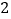 是点
是点 出发
出发 秒后
秒后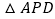 的面积
的面积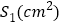 与
与 (秒)的函数关系图象;图
(秒)的函数关系图象;图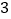 是点
是点 出发
出发 秒后
秒后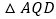 的面积
的面积 与
与 (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象: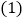 求
求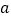 、
、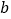 、
、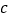 的值;
的值; 设点
设点 出发
出发 (秒)后离开点
(秒)后离开点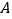 的路程为
的路程为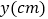 ,请写出
,请写出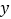 与
与 的函数关系式,并求出点
的函数关系式,并求出点 与
与 相遇时
相遇时 的值.
的值.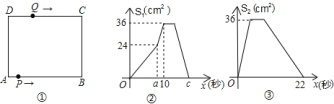
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )

A.1.8
B.2.4
C.3.2
D.3.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
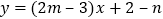 满足下列条件,分别求出
满足下列条件,分别求出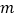 ,
, 的取值范围.
的取值范围.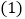 使得
使得 随
随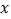 增加而减小.
增加而减小.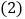 使得函数图象与
使得函数图象与 轴的交点在
轴的交点在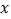 轴的上方.
轴的上方.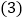 使得函数图象经过一、三、四象限.
使得函数图象经过一、三、四象限. -
科目: 来源: 题型:
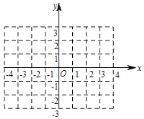
查看答案和解析>>【题目】已知一次函数
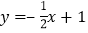 ,它的图象与
,它的图象与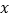 轴交于点
轴交于点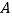 ,与
,与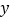 轴交于点
轴交于点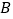 .
.
 点
点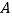 的坐标为________,点
的坐标为________,点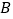 的坐标为________;
的坐标为________; 画出此函数图象;
画出此函数图象; 画出该函数图象向下平移
画出该函数图象向下平移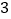 个单位长度后得到的图象;
个单位长度后得到的图象;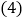 写出一次函数
写出一次函数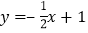 图象向下平移
图象向下平移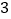 个单位长度后所得图象对应的表达式.
个单位长度后所得图象对应的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )

A. 5对 B. 6对 C. 7对 D. 8对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
相关试题

