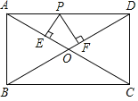
【题目】已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
首先连接OP.由矩形ABCD的两边AB=5,BC=12,可求得OA=OD=![]() ,然后由S△AOD=S△AOP+S△DOP求得答案.
,然后由S△AOD=S△AOP+S△DOP求得答案.
解:如图,连接PO, 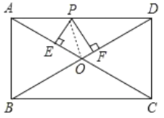
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=ABBC=60,OA=OC,OB=OD,AC=BD,
AC=![]() ,
,
∴S△AOD=![]() S矩形ABCD=15,OA=OD=
S矩形ABCD=15,OA=OD=![]() AC=
AC=![]() ,
,
∴S△AOD=S△AOP+S△DOP=![]() OAPE+
OAPE+![]() ODPF=
ODPF=![]() OA(PE+PF)=
OA(PE+PF)=![]() ×
×![]() ×(PE+PF)=15,
×(PE+PF)=15,
∴PE+PF=![]() ,
,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是射线BM上的一个动点(点P不与点B重合),∠AOB= 30°,∠ABM=60°.当∠OAP=______时,以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种电子产品共4件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
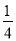 .
.(1)该批产品有正品________件;
(2)如果从中任意取出2件,利用列表或树状图求取出2件都是正品的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
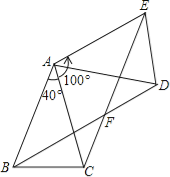
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
-
科目: 来源: 题型:
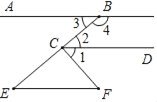
查看答案和解析>>【题目】把下面的推理过程补充完整,并在括号内填上理由.
已知:B、C、E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
试说明:∠BCF=∠E+∠F
解:∵∠3=∠E(已知)
∴EF∥ (内错角相等,两直线平行)
∵∠4+∠2=180°(已知)
∴CD∥
∴CD∥ (平行于同一条直线的两条直线互相平行)
∴∠1=∠F,
∠2=
∵∠BCF=∠1+∠2(已知)
∴∠BCF=∠E+∠F(等量代换)
-
科目: 来源: 题型:
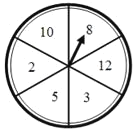
查看答案和解析>>【题目】小亮、小颖的手上都有两根长度分别为5、8的木棒,小亮与小颖都想通过转动转盘游戏来获取第三根木棒,如图,一个均匀的转盘被平均分成6等份,分别标有木棒的长度2,3,5,8,10,12这6个数字.小亮与小颖各转动转盘一次,停止后,指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜,三根木棒能组成等腰三角形则小颖获胜.
(1)小亮获胜的概率是 ;
(2)小颖获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,她连续转动转盘10次,都没转到5和8,能不能就说小颖获胜的可能性为0?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=
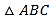 (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=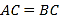 .
.(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
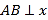
相关试题

