【题目】如图1,数轴上的点A,B.C依次表示数-2,x,4.某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点B,发现点A对齐刻度1.8cm,点C对齐刻度5.4cm.
(1)AC= 个单位长度;由图可知数轴上的一个单位长度对应刻度尺上的 cm;数轴上的点B表示数 ;

(2)已知T是数轴上一点(不与点A、点B、点C重合),点P表示的数是t,点P是线段BT的三等分点,且TP=2BP.
①如图3,当-2<t<4时,试试猜想线段CT与AP的数量关系,并说明理由;
②若|2BT-3AP|=1,请直接写出所有满足条件的t的值.

参考答案:
【答案】(1)6,0.6,-5;(2)猜想:AP=![]() CT,证明见解析;(3)t=-15或t=-13或t=-
CT,证明见解析;(3)t=-15或t=-13或t=-![]() 或t=-
或t=-![]() .
.
【解析】
(1)根据两点间的距离解答即可;
(2)①先根据P是线段BT的三等分点得:BP=![]() BT=
BT=![]() (t+5),再根据两点间的距离分别表示CT和AP的长解答即可;
(t+5),再根据两点间的距离分别表示CT和AP的长解答即可;
②分四种情况进行讨论,根据|2BT-3AP|=1列方程解答即可.
(1)AC=4-(-2)=6(个单位长度),
AC=5.4-1.8=3.6cm,
![]() ,
,
即数轴上的一个单位长度对应刻度尺上的0.6cm,
∴1.8=0.6(-2-x),
x=-5,
即数轴上的点B表示-5,
故答案为:6;0.6;-5;
(2)①如图3,猜想:![]() ,
,
理由是:∵TP=2BP,
∴![]() ,
,
∵AB=-2-(-5)=3,
∴![]() ,
,
∴CT=4-t,
∴![]() ;
;
②分四种情况:
i)如图4,当t>4,则点P在A的右边,

∴BT=t+5,![]() ,
,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
![]() 或
或![]() ,
,
解得:t=-13(不符合题意),t=-15(不符合题意),
ii)如图3,当-2<t<4时,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
由①得:![]() ,
,
解得:![]() ,
,
或![]() ,
,
解得:![]() (不符合题意),
(不符合题意),
iii)如图5,当-5<t<-2时,

∴BT=t+5,![]() ,
,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
由①得:![]() ,
,
解得:![]() (不符合题意),
(不符合题意),
或![]() ,
,
解得:![]() ,
,
iiii)如图6,当t<-5时,

∴BT=-5-t,![]() ,
,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
![]() ,
,
解得:t=-15,
或![]() ,
,
解得:t=-13,
综上,t=-15或t=-13或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=
 ,直线AC解析式为y2=ax+b.
,直线AC解析式为y2=ax+b.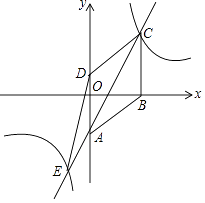
(1)求反比例函数解析式;
(2)当y1<y2时,求x的取值范围;
(3)求△CDE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司租用两种型号的货车各一辆,分別将产品运往甲市与乙市(运费收费标准如下表),已知该公司到乙市的距离比到甲市的距离远30km,B车的总运费比A车的总运费少1080元.
(1)求这家公司分别到甲、乙两市的距离;
(2)若A,B两车同时从公司出发,其中B车以60km/h的速度匀速驶向乙市,而A车根据路况需要,先以45kmh的速度行驶了3小吋,再以75km/h的速度行驹到达甲市.
①在行驶的途中,经过多少时间,A,B两车到各自目的地的距离正好相等?
②若公司希望B车能与A车同吋到达目的地,B车必须在以60km/h的速度行驶一段时间后提速,若提速后的速度为70km/h(速度从60km/h提速到70km/h的时间忽略不汁),则B车应该在行驶 小时后提速.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.

(1)求证:AC平分∠FAD;
(2)已知AF=3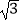 ,求阴影部分面积.
,求阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点B在线段AC上,点D在线段AB上.
(1)如图1,若AB=6cm,BC=4cm,D为线段AC的中点,求线段DB的长度;
(2)如图2,若BD=
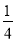 AB=
AB=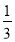 CD,E为线段AB的中点,EC=12cm,求线段AC的长度.
CD,E为线段AB的中点,EC=12cm,求线段AC的长度.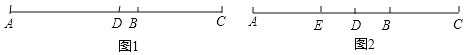
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
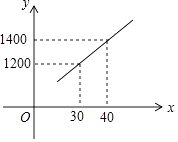
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
相关试题

