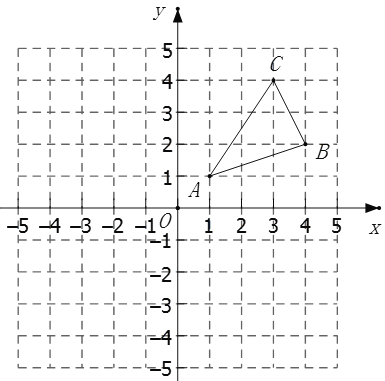
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
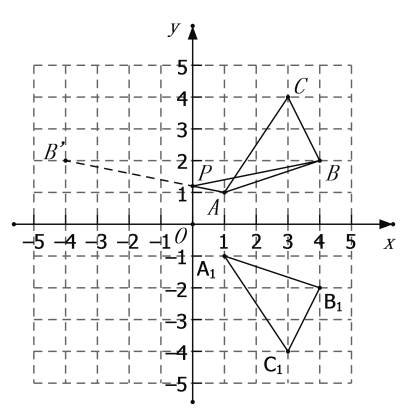
(1)请画出![]() 关于
关于![]() 轴成轴对称的图形
轴成轴对称的图形![]() ,并写出
,并写出![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)求![]() 的面积;
的面积;
(3〉在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,请画出点
的值最小,请画出点![]() 的位置.
的位置.
参考答案:
【答案】(1)图见解析;![]() 的坐标为
的坐标为![]() 、
、![]() 的坐标为
的坐标为![]() 、
、![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据网格结构找出点A、B、C关于y轴的对称的点A1、B1、C1的位置,然后顺次连接即可;
(2)依据割补法即可得到△ABC的面积.
(3)找出点B关于y轴的对称点B′,连接B′A与x轴相交于一点,根据轴对称确定最短路线问题,交点即为所求的点P的位置.
解:(1)△A1B1C1如图所示,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ;
;
(2)![]()
(3)如图所示,作点B关于y轴的对称点B',连接B'A,交y轴于点P,则PA+PB最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 交
交 于点
于点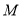 ,交
,交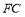 于点
于点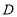 ,
,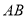 交
交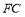 于点
于点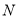 ,
,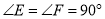 ,
,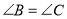 ,
,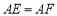 ,给出下列结论:①
,给出下列结论:①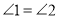 ;②
;②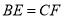 ;③
;③ ;④
;④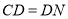 ;⑤
;⑤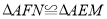 .其中正确的结论有( )
.其中正确的结论有( )
A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某共享单车公司提供了手机和会员卡两种支付方式.若用手机支付方式,骑行时间在半小时以内(含半小时)不收费,超出半小时后每半小时收费1元,若选择会员卡支付,骑行时间每半小时收费0.8元,设骑行时间为x小时.
(1)根据题意,填写下表(单位:元):
骑行时间(小时)
0.5
2
3
…
手机支付付款金额(元)
0
…
会员卡支付付款金额(元)
3.2
…
(2)设用手机支付付款金额为y1元,用会员卡支付付款金额为y2元,分别写出y1,y2关于x的函数关系式;
(3)若李老师经常骑行该公司的共享单车,他应选择哪种支付方式比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=
 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)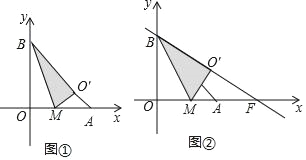
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC、AC上.
(I)求抛物线的解析式;
(II)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(III)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF.若点M在抛物线上,求k的值.
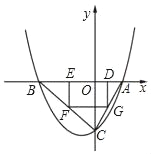
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为
 的正方形中剪掉一个边长为
的正方形中剪掉一个边长为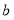 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).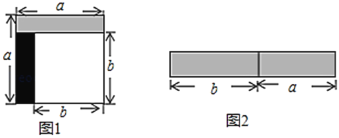
(1)探究:上述操作能验证的等式是:(请选择正确的一个)
A.
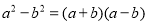 B.
B. C.
C.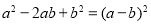
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知
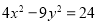 ,
,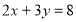 ,求
,求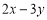 的值;
的值;②计算:
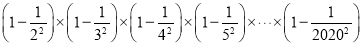 .
.
相关试题

