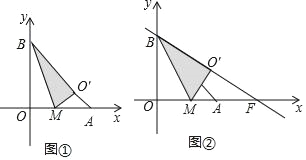
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=![]() 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)
参考答案:
【答案】(Ⅰ)O'(![]() ,2﹣
,2﹣![]() );(Ⅱ)①F(2
);(Ⅱ)①F(2![]() ,0);②F(
,0);②F(![]() ,0)
,0)
【解析】
(I) 过点O'作O'H⊥y轴于H,由折叠可知,BO'=BO=2,∠BO'H=∠BAO=45°,利用特殊角的三角函数值求出BH、O'H,从而得到O'的坐标;
(II) ①由BA平分∠MBF时,得到∠OBF=60,利用特殊角的三角函数值求出OF,即可得到点F的坐标;②先说明△FO'M∽△FOB,从而![]() =
=![]() ,设F(a,0),利用勾股定理,用含a式子表示O'F,代入
,设F(a,0),利用勾股定理,用含a式子表示O'F,代入![]() =
=![]() ,求出a,从而得到点F的坐标.
,求出a,从而得到点F的坐标.
解:(I)如图①,过点O'作O'H⊥y轴于H,
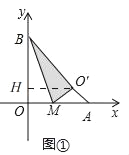
由折叠知,△BMO≌△BMO',
∴BO'=BO=2,
∵O'H∥OA,
∴∠BO'H=∠BAO=45°,
在Rt△BO'H中,O'H=BO'cos∠BO'H=![]() ,
,
∴BH=O'H=![]() ,
,
∴OH=OB﹣BH=2﹣![]() ,
,
∴O'(![]() ,2﹣
,2﹣![]() );
);
(II)①∵BA平分∠MBF,
∴∠ABO=3∠MBA=45°,
∴∠ABF=∠MBA=15°,
∴∠OBF=∠ABO+∠ABF=60°,
在Rt△BOF中,OF=OBtan60=2![]() ,
,
∴F(2![]() ,0);
,0);
②由折叠知,O'M=OM=![]() ,O'B=OB=2,∠MO'F=90°=∠FOB,
,O'B=OB=2,∠MO'F=90°=∠FOB,
∵∠FO'M=∠FOB,
∴△FO'M∽△FOB,
∴![]() =
=![]() ,
,
设F(a,0)(a>0),
∴OF=a,
在Rt△BOF中,BF=![]() ,
,
∴O'F=![]() ﹣2,
﹣2,
∴![]() ,
,
∴a=0(舍)或a=![]() ,
,
F(![]() ,0).
,0).
故答案为:(I)O'(![]() ,2﹣
,2﹣![]() );(II)①F(2
);(II)①F(2![]() ,0);②F(
,0);②F(![]() ,0)
,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 交
交 于点
于点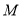 ,交
,交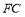 于点
于点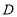 ,
,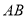 交
交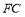 于点
于点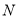 ,
,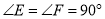 ,
,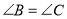 ,
,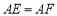 ,给出下列结论:①
,给出下列结论:①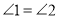 ;②
;②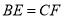 ;③
;③ ;④
;④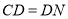 ;⑤
;⑤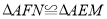 .其中正确的结论有( )
.其中正确的结论有( )
A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某共享单车公司提供了手机和会员卡两种支付方式.若用手机支付方式,骑行时间在半小时以内(含半小时)不收费,超出半小时后每半小时收费1元,若选择会员卡支付,骑行时间每半小时收费0.8元,设骑行时间为x小时.
(1)根据题意,填写下表(单位:元):
骑行时间(小时)
0.5
2
3
…
手机支付付款金额(元)
0
…
会员卡支付付款金额(元)
3.2
…
(2)设用手机支付付款金额为y1元,用会员卡支付付款金额为y2元,分别写出y1,y2关于x的函数关系式;
(3)若李老师经常骑行该公司的共享单车,他应选择哪种支付方式比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
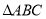 三个顶点的坐标分别为
三个顶点的坐标分别为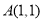 ,
,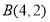 ,
,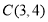 .
.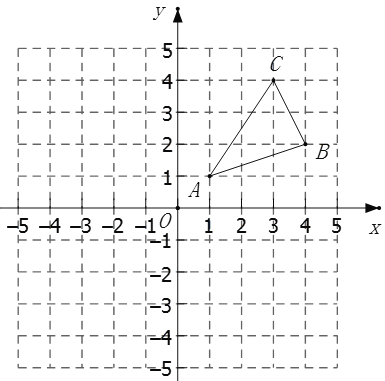
(1)请画出
 关于
关于 轴成轴对称的图形
轴成轴对称的图形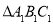 ,并写出
,并写出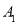 、
、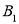 、
、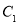 的坐标;
的坐标;(2)求
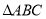 的面积;
的面积;(3〉在
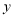 轴上找一点
轴上找一点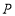 ,使
,使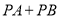 的值最小,请画出点
的值最小,请画出点 的位置.
的位置. -
科目: 来源: 题型:
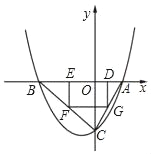
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC、AC上.
(I)求抛物线的解析式;
(II)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(III)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF.若点M在抛物线上,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为
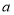 的正方形中剪掉一个边长为
的正方形中剪掉一个边长为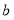 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).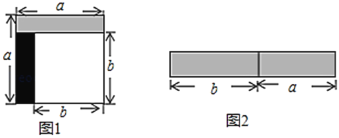
(1)探究:上述操作能验证的等式是:(请选择正确的一个)
A.
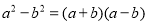 B.
B. C.
C.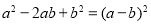
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知
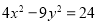 ,
,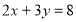 ,求
,求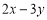 的值;
的值;②计算:
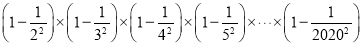 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
相关试题

