22．设函数f(x)的定义域为R，对于任意实数x，y，总有f(x+y)＝f(x)f(y)，且当x＞0时，0＜f(x)＜1．

(1)求f(0)的值；(2)证明：当x＜0时，f(x)＞1；

(3)证明：f(x)在R上单调递减；(4)若M＝{y|f(y)·f(1－a)≥f(1)}，N＝{y|f(ax²+x+1－y)＝1，x∈R}，且M∩N≠φ，求a的取值范围．

21．今有甲、乙两个篮球队进行比赛，规定两队中有一队胜4场则整个比赛宣告结束．假设甲、乙两队在每场比赛中获胜的概率都是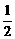．并记需要比赛的场数为ξ．

(Ⅰ)求ξ大于5的概率；

(Ⅱ)求ξ的分布列与数学期望．

20．有一块边长为4米的正方形钢板，现对其进行切割，焊接成一个长方体形无盖容器(切、焊损耗忽略不计)，有人用数学知识作了如下设计：在钢板的四个角处各切去一个小正方形，剩余部分围成一个长方体，该长方体的高为小正方形边长．

(1)请你求出这种切割、焊接而成的长方体的最大容积v₁；

(2)由于上述设计对材料有所浪费，请你重新设计，减少浪费，而且所得长方体容器的容积v₂＞v₁．

19．设a＞0，解关于x的不等式log₂＜1．

18．已知f(x)＝－4cos²x+4asinxcosx，将f(x)图象按向量＝(－，2)平移后，图象关于直线x＝对称．(1)求实数a的值，并求f(x)取得最大值时x的集合；(2)求f(x)的单调区间．

17．在△ABC中，角A、B、C的对边分别为a、b、c，已知＝(bcosc，－1)，＝((c－3a)cosB，1)，且与为共线向量，求sinB．

16．“渐升数”是指每个数字比其左边的数字大的正整数(如34689).则五位“渐升数”共有　

　　　 　个，若把这些数按从小到大的顺序排列，则第100个数为　　　　　 　.

15．若函数的表达式是　　　

14．已知偶函数f(x)在[0，+∞)上为增函数，则不等式f(2x+1)＞f(2－x)的解集为＿＿＿．

13．抛物线y＝(n²+n)x²－(2n+1)x+1(n∈N⁺)，交x轴于An，Bn两点，则|A₁B₁|+|A₂B₂|+…+|A₂₀₀₅B₂₀₀₅|的值为＿