19. 如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.

17.已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;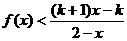 .
.
(17)已知函数f(x)=A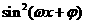 (A>0,
(A>0, >0,0<
>0,0<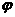 <
<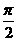 函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求 ;
;
(2)计算f(1)+f(2)+ f(3)… +f(2 007).
(18)A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
(19)(本小题满分12分)
如图,已知平面A1B1C1平行于三棱锥F-ABC的底面ABC,等边∆ AB1C所在的平面与底面ABC垂直,且 ACB=90°,设AC=2a,BC=a.
ACB=90°,设AC=2a,BC=a.
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面FBC的距离;
(3)求二面角A-FB-C的大小.
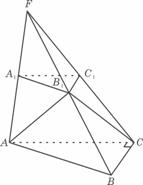
(19题图)
(20)双曲线C与椭圆 有相同的焦点,直线y=
有相同的焦点,直线y= 为C的一条渐近线.
为C的一条渐近线.
(1) 求双曲线C的方程;
(2) 过点P(0,4)的直线 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当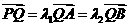 ,且
,且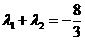 时,求Q点的坐标.
时,求Q点的坐标.
(21)已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
(3) 记bn=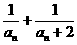 ,求{bn}数列的前项和Sn,并证明Sn+
,求{bn}数列的前项和Sn,并证明Sn+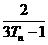 =1.
=1.

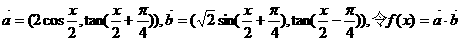 .
. 的函数
的函数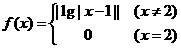 ,若
,若 则关于
则关于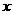 的方程
的方程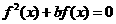 的不同实根有 ________个.
的不同实根有 ________个.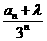 }为等差数列的实数λ=_____________
}为等差数列的实数λ=_____________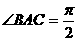 ,则PA与底面ABC所成角为
,则PA与底面ABC所成角为 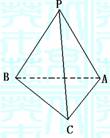 设实数x, y满足
设实数x, y满足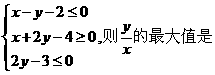 .
.