【题目】已知函数![]()
(1)若直线![]() 与曲线
与曲线![]() 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
(2)设函数![]() 在[1,2]上的值域为
在[1,2]上的值域为![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)12.(2) ![]()
【解析】试题分析:(1)先求出函数![]() 的极值,再根据直线
的极值,再根据直线![]() 与曲线
与曲线![]() 都只有两个交点得
都只有两个交点得![]() 和
和![]() 的值,然后求出四个交点的坐标,即可证明这四个交点可以构成一个平行四边形及计算出该平行四边形的面积;(2)化简
的值,然后求出四个交点的坐标,即可证明这四个交点可以构成一个平行四边形及计算出该平行四边形的面积;(2)化简![]() ,然后求导,求出
,然后求导,求出![]() 的极值,对
的极值,对![]() 进行分类讨论,求出单调性及最值,表示出
进行分类讨论,求出单调性及最值,表示出![]() ,根据
,根据![]() 的取值,即可求出
的取值,即可求出![]() 的单调性及最小值.
的单调性及最小值.
试题解析:(1)证明:令![]() 得
得![]()
令![]() 得
得![]() ;令
;令![]()
∴![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() .
.
∵![]() ,令
,令![]() 或3;
或3;
令![]()
∴这四个交点分别为(0,0),(3,0),(-1,-4),(2,-4)
∵3-0=2-(-1)=3
∴这四个交点可以构成一个平行四边形,且其面积为![]()
(2)解:因为![]()
所以![]()
令![]() ,得
,得![]() 或
或![]() ,
,
①当![]() 时,
时,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
又因为![]() ,所以
,所以![]()
所以![]()
因为![]()
所以![]() 在
在![]() 上单调递减,所以当
上单调递减,所以当![]() 时,
时, ![]() 的最小值为
的最小值为![]()
②当![]() 时,
时,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
又因为![]() ,所以
,所以![]()
所以![]()
因为![]()
所以![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时, ![]()
③当![]() 时,
时,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
所以![]()
所以![]()
因为![]()
所以![]() 在
在![]() 上的最小值为
上的最小值为![]()
综上, ![]() 的最小值为
的最小值为![]()
点睛:本题考查利用导数研究函数的单调性与最值,对数函数的性质及分类讨论思想,利用导数研究函数的单调性时要注意先求函数的定义域,若所求的导数含有参数,在进行讨论时要做到分类标准统一,对参数的讨论要不重不漏.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是梯形,四边形
是梯形,四边形 是矩形,且平面
是矩形,且平面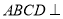 平面
平面 ,
,  ,
,  ,
,  ,
,  是线段
是线段 上的动点.
上的动点.
(1)试确定点
 的位置,使
的位置,使 平面
平面 ,并说明理由;
,并说明理由;(2)在(1)的条件下,求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =
= 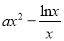 ,
, 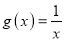 .
.(1)若函数
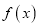 在
在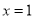 处取得极值,求
处取得极值,求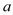 的值,并判断
的值,并判断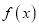 在
在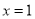 处取得极大值还是极小值.
处取得极大值还是极小值.(2)若
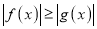 在
在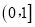 上恒成立,求
上恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )

A.40m
B.20m
C.305m
D.(20 ﹣40)m
﹣40)m -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是
甲
0
1
0
2
2
0
3
1
2
4
乙
2
3
1
1
0
2
1
1
0
1
由此判断性能较好的一台是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
0.025
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
②
[145,155]
0.050
合计
③
(1)根据图表,①②③处的数值分别为、、;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面多边形
 中,四边形
中,四边形 为正方形,
为正方形,  ,
,  ,沿着
,沿着 将图形折成图2,其中
将图形折成图2,其中 ,
,  ,
,  为
为 的中点.
的中点.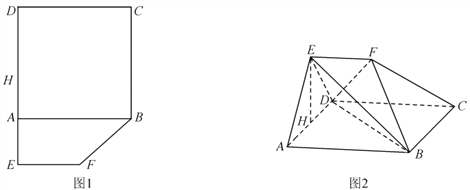
(1)求证:
 ;
;(2)求四棱锥
 的体积.
的体积.
相关试题

