【题目】已知函数![]() =
= ![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值,并判断
的值,并判断![]() 在
在![]() 处取得极大值还是极小值.
处取得极大值还是极小值.
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由![]() 得到
得到![]() ,并通过求导判断得到
,并通过求导判断得到![]() 处取得极小值;(2)
处取得极小值;(2)![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,通过分类讨论,得到
,通过分类讨论,得到![]() 时,
时, 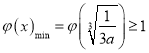 ,所以
,所以![]() 。
。
试题解析:
(1)![]() 的定义域是
的定义域是![]() ,
,![]() =
=![]() ,由
,由![]() 得
得![]() .
.
当![]() 时,
时,![]() =
=![]() ,
,![]() =
=![]()
![]()
![]()
![]() 恒成立,
恒成立,![]() 令
令![]() =
=![]() ,
,![]() =
=![]()
![]() 恒成立
恒成立
![]()
![]() 在
在![]() 上单调递增,又因为
上单调递增,又因为![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
![]() 当
当![]() 时,
时,![]() 在
在![]() 处取得极小值.
处取得极小值.
(2)由![]() 得
得![]() 在
在![]() 上恒成立
上恒成立
即![]() 在
在![]() 上恒成立.
上恒成立.
解法一(将绝对值看成一个函数的整体进行研究):
令![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,所以
,所以![]() 的值域为:
的值域为:![]() ,因为
,因为![]() ,所以
,所以![]() 的值域为
的值域为![]() ;所以不成立.
;所以不成立.
②当![]() 时,易知
时,易知![]() 恒成立.
恒成立.![]() ,所以
,所以![]() 在
在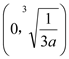 上单调递减,在
上单调递减,在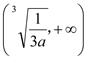 上单调递增.因为
上单调递增.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在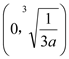 上单调递减,在
上单调递减,在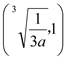 上单调递增.所以
上单调递增.所以![]()
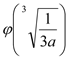 ,依题意,
,依题意,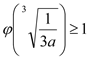 ,所以
,所以![]() .
.
综上:![]()
解法二(求命题的否定所对应的集合,再求该集合的补集):
命题“![]() 对
对![]() 都成立”的否定是“
都成立”的否定是“![]() 在
在![]() 上有解”
上有解”
![]() 在
在![]() 上有解
上有解![]()
![]() 在
在![]() 上有解
上有解
![]()
![]() 在
在![]() 上有解
上有解
令![]() ,
,![]() .
.
![]()
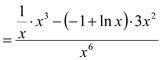
![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]()
![]() ,所以
,所以![]() 无最小值.所以
无最小值.所以![]() ;
;
令![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() ,所以
,所以![]() .
.
因为![]() 在
在![]() 上有解时,
上有解时,![]() ;
;
所以![]() 对
对![]() 都成立时,
都成立时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M:x2+(y﹣2)2=r2(r>0)与曲线C:(y﹣2)(3x﹣4y+3)=0有三个不同的交点.
(1)求圆M的方程;
(2)已知点Q是x轴上的动点,QA,QB分别切圆M于A,B两点. ①若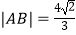 ,求|MQ|及直线MQ的方程;
,求|MQ|及直线MQ的方程;
②求证:直线AB恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
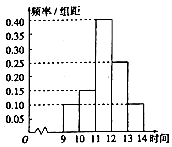
A.100万元
B.10万元
C.7.5万元
D.6.25万元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是梯形,四边形
是梯形,四边形 是矩形,且平面
是矩形,且平面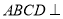 平面
平面 ,
,  ,
,  ,
,  ,
,  是线段
是线段 上的动点.
上的动点.
(1)试确定点
 的位置,使
的位置,使 平面
平面 ,并说明理由;
,并说明理由;(2)在(1)的条件下,求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )

A.40m
B.20m
C.305m
D.(20 ﹣40)m
﹣40)m -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若直线
 与曲线
与曲线 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;(2)设函数
 在[1,2]上的值域为
在[1,2]上的值域为 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是
甲
0
1
0
2
2
0
3
1
2
4
乙
2
3
1
1
0
2
1
1
0
1
由此判断性能较好的一台是 .
相关试题

