【题目】如图1,在平面多边形![]() 中,四边形
中,四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,沿着
,沿着![]() 将图形折成图2,其中
将图形折成图2,其中![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
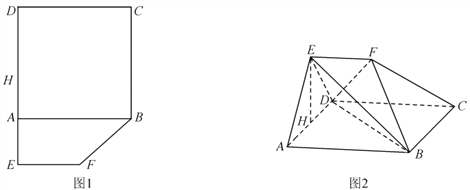
(1)求证: ![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析;(2)1.
【解析】试题分析:(1) 由题可知, ![]() ,
, ![]() ,且
,且![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,进而得到
,进而得到![]() ,又
,又![]() ,可证出
,可证出![]() 平面
平面![]() ,则
,则![]() ;(2)将四棱锥分割,
;(2)将四棱锥分割, ![]() , 因为
, 因为![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() ,计算三棱锥E-ABD的体积即可.
,计算三棱锥E-ABD的体积即可.
试题解析:
(1)证明:由题可知, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
, ![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解: ![]() ,其中
,其中![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
所以![]() .
.
点睛: 求锥体的体积要充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解,注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若直线
 与曲线
与曲线 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;(2)设函数
 在[1,2]上的值域为
在[1,2]上的值域为 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是
甲
0
1
0
2
2
0
3
1
2
4
乙
2
3
1
1
0
2
1
1
0
1
由此判断性能较好的一台是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
0.025
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
②
[145,155]
0.050
合计
③
(1)根据图表,①②③处的数值分别为、、;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合P={x|2x2﹣5x+2≤0},函数y=log2(ax2+2)的定义域为S
(1)若P∩S≠,求实数a的取值范围
(2)若方程log2(ax2+2)=2在 上有解,求实数a的取值范围.
上有解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 过抛物线焦点,且与抛物线交于
过抛物线焦点,且与抛物线交于 ,
,  两点,以线段
两点,以线段 为直径的圆与抛物线准线的位置关系是( )
为直径的圆与抛物线准线的位置关系是( )A. 相离 B. 相交 C. 相切 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)将一颗骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,以分别得到的点数(m,n)作为点P的坐标(m,n),求:点P落在区域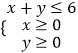 内的概率;
内的概率;
(2)在区间[1,6]上任取两个实数(m,n),求:使方程x2+mx+n2=0有实数根的概率.
相关试题

