搜索
【题目】要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，则电视塔的高度为（ ） 
A.40m
B.20m
C.305m
D.（20 
﹣40）m
参考答案：
【答案】A
【解析】解：由题题意，设AB=x，则BD= 
x，BC=x 在△DBC中，∠BCD=120°，CD=40，
∴根据余弦定理，得BD2=BC2+CD2﹣2BCCDcos∠DCB
即：（ x）2=（40）2+x2﹣2×40xcos120°
整理得x2﹣20x﹣800=0，解之得x=40或x=﹣20（舍去）
即所求电视塔的高度为40米．
故选：A．
设出AB=x，由题意将BD、DC用x来表示，然后在△DBC中利用余弦定理建立方程求得x，即可得到电视塔的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一商场在某日促销活动中，对9时至14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时至12时的销售为（ ）
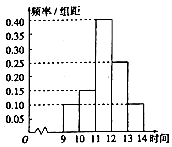
A.100万元
B.10万元
C.7.5万元
D.6.25万元 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形
是梯形，四边形
是矩形，且平面
平面
， 
， 
， 
， 
是线段
上的动点.
（1）试确定点
的位置，使
平面
，并说明理由；（2）在（1）的条件下，求平面
与平面
所成锐二面角的余弦值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
= 
， 
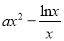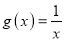.（1）若函数
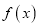在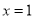
处取得极值，求
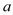的值，并判断
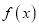在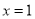
处取得极大值还是极小值.（2）若
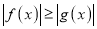在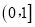
上恒成立，求
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
（1）若直线
与曲线
都只有两个交点，证明：这四个交点可以构成一个平行四边形，并计算该平行四边形的面积；（2）设函数
在[1，2]上的值域为
，求
的最小值. -
科目： 来源： 题型：
查看答案和解析>>【题目】甲乙两台机床同时生产一种零件，10天中，两台机床每天出的次品数分别是
甲
0
1
0
2
2
0
3
1
2
4
乙
2
3
1
1
0
2
1
1
0
1
由此判断性能较好的一台是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】高二年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：
分组
频数
频率
[85，95）
①
0.025
[95，105）
0.050
[105，115）
0.200
[115，125）
12
0.300
[125，135）
0.275
[135，145）
4
②
[145，155]
0.050
合计
③
（1）根据图表，①②③处的数值分别为、、；
（2）在所给的坐标系中画出[85，155]的频率分布直方图；
（3）根据题中信息估计总体落在[125，155]中的概率．
相关试题
