【题目】选修4-1:几何证明选讲
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
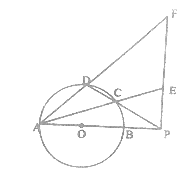
(1)当![]() 时,求
时,求![]() 的度数;
的度数;
(2)求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)24.
;(2)24.
【解析】
试题分析:(1)连接![]() ,可知
,可知![]() ,从而得到
,从而得到![]() ,进一步得到
,进一步得到![]() 的值;
的值;
(2)由(1)可知![]() ,所以点
,所以点![]() 四点共圆,那么
四点共圆,那么![]() .
.
试题解析:(1)连接BC,∵AB是圆O的直径,∴![]() ACB=90°,
ACB=90°,
又![]() APF=90°,
APF=90°,![]() CAB+
CAB+![]() CBA=
CBA=![]() EAP+
EAP+![]() PEC,
PEC,
∴![]() CBA=
CBA=![]() PEC,∵
PEC,∵![]() PEC=60°,∴
PEC=60°,∴![]() PDF=
PDF=![]() CBA=
CBA=![]() PEC=60°.
PEC=60°.
(2)由(1)知![]() PDF=
PDF=![]() PEC,
PEC,
∴D、C、E、F四点共圆,∴![]() ,
,
∵PC、PA都是圆O的割线,∴![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)求函数
 最值;
最值;(2)若
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
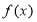 满足
满足 (
(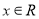 ),且
),且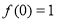 .
.(1)求
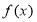 的解析式;
的解析式;(2)若函数
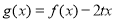 在区间
在区间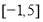 上是单调函数,求实数
上是单调函数,求实数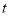 的取值范围;
的取值范围;(3)若关于
 的方程
的方程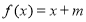 有区间
有区间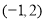 上有一个零点,求实数
上有一个零点,求实数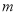 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
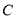 :
: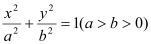 的离心率为
的离心率为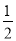 ,左顶点
,左顶点 .
.(Ⅰ)求椭圆
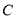 的标准方程;
的标准方程;(Ⅱ)设直线
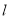 :
: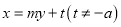 与椭圆
与椭圆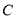 交于不同两点
交于不同两点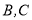 ,且满足
,且满足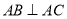 .求证:直线
.求证:直线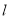 恒过定点,并求出定点
恒过定点,并求出定点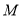 的坐标;
的坐标;(Ⅲ)在(Ⅱ)的条件下,过
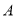 作
作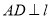 ,垂足为
,垂足为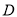 ,求
,求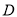 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 .
.(1)求椭圆C的离心率;
(2)设O为原点,若点A在椭圆上,点B在直线x=4上,且
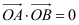 ,求直线AB截圆
,求直线AB截圆 所得弦长
所得弦长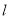 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】写出1×2×3×4×5×6×7的一个算法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面上的两个向量
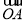 ,
,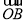 满足
满足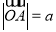 ,
,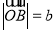 ,且
,且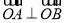 ,
, .向量
.向量 ,且
,且 .
.(1)如果点
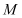 为线段
为线段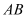 的中点,求证:
的中点,求证: 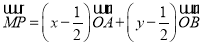 ;
;(2)求
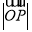 的最大值,并求此时四边形
的最大值,并求此时四边形 面积的最大值.
面积的最大值.
相关试题

