【题目】平面上的两个向量![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,
,![]() .向量
.向量![]() ,且
,且 .
.
(1)如果点![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() ;
;
(2)求![]() 的最大值,并求此时四边形
的最大值,并求此时四边形![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)证明见解析;(2)![]() ,
,![]() .
.
【解析】
试题分析:(1)由因为点![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,连同已知代入
,连同已知代入![]() 即可证明;(2)设点
即可证明;(2)设点![]() 为线段
为线段![]() 的中点,则由
的中点,则由![]() ,知
,知![]() ,又由(1)及题设条件得
,又由(1)及题设条件得![]() ,从而可判断
,从而可判断![]() 、
、![]() 、
、![]() 、
、![]() 四点都在以
四点都在以![]() 为圆心、
为圆心、![]() 为半径的圆上,已知
为半径的圆上,已知![]() 为圆
为圆![]() 的直径,得到
的直径,得到![]() ,再利用基本不等式,即可求解四边形面积的最大值.
,再利用基本不等式,即可求解四边形面积的最大值.
试题解析:(1)证明:因为点![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
所以![]() .
.
(2)解:设点![]() 为线段
为线段![]() 的中点,
的中点,
则由![]() ,知
,知![]() .
.
又由(1)及 ,得
,得
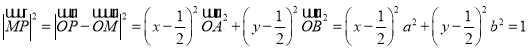
所以![]() .
.
故![]() 、
、![]() 、
、![]() 、
、![]() 四点都在以
四点都在以![]() 为圆心、
为圆心、![]() 为半径的圆上,
为半径的圆上,
所以当且仅当![]() 为圆
为圆![]() 的直径时,
的直径时,![]() .
.
这时四边形![]() 为矩形,
为矩形,
则![]() ,
,
当且仅当![]() 时,四边形
时,四边形![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-1:几何证明选讲
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
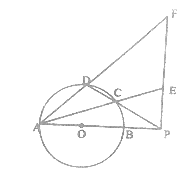
(1)当
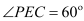 时,求
时,求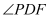 的度数;
的度数;(2)求
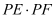 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 .
.(1)求椭圆C的离心率;
(2)设O为原点,若点A在椭圆上,点B在直线x=4上,且
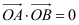 ,求直线AB截圆
,求直线AB截圆 所得弦长
所得弦长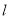 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】写出1×2×3×4×5×6×7的一个算法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程
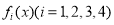 关于时间
关于时间
 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
, ,有以下结论:
,有以下结论:①当
 时,甲走在最前面;
时,甲走在最前面;②当
 时,乙走在最前面;
时,乙走在最前面;③当
 时,丁走在最前面,当
时,丁走在最前面,当 时,丁走在最后面;
时,丁走在最后面;④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列算法语句,当输入x为60时,输出y的值为
INPUT x
IF x<=50 THEN
y=0.5*x
ELSE
y=25+0.6*(x–50)
END IF
PRINT y
END
A. 25 B. 30 C. 31 D. 61
-
科目: 来源: 题型:
查看答案和解析>>【题目】读下面的程序:
i=1
S=0
DO
INPUT x
S=S+x
i=i+1
LOOP UNTIL i>10
A=S/10
PRINT A
END
该程序的作用是
A. 计算9个数的和 B. 计算9个数的平均数
C. 计算10个数的和 D. 计算10个数的平均数
相关试题

