【题目】已知![]() .
.
(1)求函数![]() 最值;
最值;
(2)若![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1) ![]() 取最大值
取最大值![]() ,无最小值;(2)详见解析.
,无最小值;(2)详见解析.
【解析】
试题分析:(1)分析函数的导数,并且求函数的极值点,并且分析极值点两侧的单调性,求函数的最值;
(2)设![]() ,根据(1)可知
,根据(1)可知![]() ,然后采用分析法的证明思路,转化为证明
,然后采用分析法的证明思路,转化为证明![]() ,设
,设![]() ,
,![]() ,根据函数的导数,可知函数是单调递增函数,所以
,根据函数的导数,可知函数是单调递增函数,所以![]() ,得证.
,得证.
试题解析:(1)对![]() 求导可得
求导可得![]() ,
,
令![]() 得x=0.
得x=0.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当x=0时,![]() 取最大值
取最大值![]() ,无最小值.
,无最小值.
(2)不妨设![]() ,由(1)得
,由(1)得
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
若![]() ,则
,则![]() ,
,
欲证:![]() ,只需证:
,只需证:![]() ,
,
∵![]() 函数
函数![]() 在
在![]() 单调递减,
单调递减,
只需证:![]() ,考虑到
,考虑到![]() ,即证
,即证![]() ,也即证
,也即证![]()
下证:![]() ,
,
设![]() ,
,
![]() ,
,
∴![]() ,故g(x)在
,故g(x)在![]() 上单调递增,
上单调递增,
故![]() 时,g(x)<g(0)=0,即f(x)-f(-x)<0,∴
时,g(x)<g(0)=0,即f(x)-f(-x)<0,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面 ,
, ,
, 为
为 中点,底面
中点,底面 是直角梯形,
是直角梯形, ,
,
 ,
, ,
, .
.(1)求证:
 平面
平面 ;
;(2)求证:平面
 平面
平面 ;
;(3)设
 为棱
为棱 上一点,
上一点, ,试确定
,试确定 的值使得二面角
的值使得二面角 为
为 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
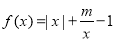 (
(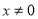 ).
).(1)当
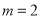 时,判断
时,判断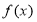 在
在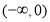 的单调性,并用定义证明.
的单调性,并用定义证明.(2)若对任意
 ,不等式
,不等式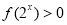 恒成立,求
恒成立,求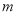 的取值范围;
的取值范围;(3)讨论
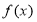 的零点个数.
的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列三句话按三段论的模式排列顺序正确的是( )
① 2018能被2整除;②一切偶数都能被2整除;③ 2018是偶数;
A. ①②③ B. ②①③ C. ②③① D. ③②①
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
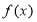 满足
满足 (
(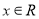 ),且
),且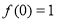 .
.(1)求
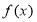 的解析式;
的解析式;(2)若函数
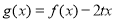 在区间
在区间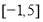 上是单调函数,求实数
上是单调函数,求实数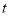 的取值范围;
的取值范围;(3)若关于
 的方程
的方程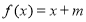 有区间
有区间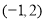 上有一个零点,求实数
上有一个零点,求实数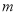 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
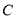 :
: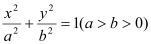 的离心率为
的离心率为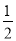 ,左顶点
,左顶点 .
.(Ⅰ)求椭圆
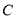 的标准方程;
的标准方程;(Ⅱ)设直线
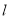 :
: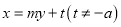 与椭圆
与椭圆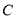 交于不同两点
交于不同两点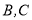 ,且满足
,且满足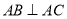 .求证:直线
.求证:直线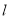 恒过定点,并求出定点
恒过定点,并求出定点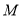 的坐标;
的坐标;(Ⅲ)在(Ⅱ)的条件下,过
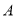 作
作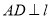 ,垂足为
,垂足为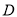 ,求
,求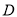 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-1:几何证明选讲
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
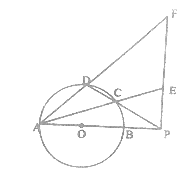
(1)当
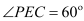 时,求
时,求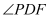 的度数;
的度数;(2)求
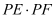 的值.
的值.
相关试题

