【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(﹣1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
参考答案:
【答案】
(1)解:求导数可得f′(x)= ![]() ﹣a
﹣a
∵f(x)在(1,+∞)上是单调减函数,∴ ![]() ﹣a≤0在(1,+∞)上恒成立,
﹣a≤0在(1,+∞)上恒成立,
∴a≥ ![]() ,x∈(1,+∞).
,x∈(1,+∞).
∴a≥1.
令g′(x)=ex﹣a=0,得x=lna.当x<lna时,g′(x)<0;当x>lna时,g′(x)>0.
又g(x)在(1,+∞)上有最小值,所以lna>1,即a>e.
故a的取值范围为:a>e.
(2)解:当a≤0时,g(x)必为单调函数;当a>0时,令g′(x)=ex﹣a>0,解得a<ex,即x>lna,
因为g(x)在(﹣1,+∞)上是单调增函数,类似(1)有lna≤﹣1,即0< ![]() .结合上述两种情况,有
.结合上述两种情况,有 ![]() .
.
①当a=0时,由f(1)=0以及f′(x)= ![]() >0,得f(x)存在唯一的零点;
>0,得f(x)存在唯一的零点;
②当a<0时,由于f(ea)=a﹣aea=a(1﹣ea)<0,f(1)=﹣a>0,且函数f(x)在[ea,1]上的图象不间断,所以f(x)在(ea,1)上存在零点.
另外,当x>0时,f′(x)= ![]() ﹣a>0,故f(x)在(0,+∞)上是单调增函数,所以f(x)只有一个零点.
﹣a>0,故f(x)在(0,+∞)上是单调增函数,所以f(x)只有一个零点.
③当0<a≤ ![]() 时,令f′(x)=
时,令f′(x)= ![]() ﹣a=0,解得x=
﹣a=0,解得x= ![]() .当0<x<
.当0<x< ![]() 时,f′(x)>0,当x>
时,f′(x)>0,当x> ![]() 时,f′(x)<0,
时,f′(x)<0,
所以,x= ![]() 是f(x)的最大值点,且最大值为f(
是f(x)的最大值点,且最大值为f( ![]() )=﹣lna﹣1.
)=﹣lna﹣1.
(i)当﹣lna﹣1=0,即a= ![]() 时,f(x)有一个零点x=e;
时,f(x)有一个零点x=e;
(ii)当﹣lna﹣1>0,即0<a< ![]() 时,f(x)有两个零点;
时,f(x)有两个零点;
实际上,对于0<a< ![]() ,由于f(
,由于f( ![]() )=﹣1﹣
)=﹣1﹣ ![]() <0,f(
<0,f( ![]() )>0,且函数f(x)在[
)>0,且函数f(x)在[ ![]() ]上的图象不间断,所以f(x)在(
]上的图象不间断,所以f(x)在( ![]() )上存在零点.
)上存在零点.
另外,当0<x< ![]() 时,f′(x)=
时,f′(x)= ![]() ﹣a>0,故f(x)在(0,
﹣a>0,故f(x)在(0, ![]() )上时单调增函数,所以f(x)在(0,
)上时单调增函数,所以f(x)在(0, ![]() )上只有一个零点.
)上只有一个零点.
下面考虑f(x)在( ![]() ,+∞)上的情况,先证明f(
,+∞)上的情况,先证明f( ![]() )=a(
)=a( ![]() )<0.
)<0.
为此,我们要证明:当x>e时,ex>x2.设h(x)=ex﹣x2,则h′(x)=ex﹣2x,再设l(x)=h′(x)=ex﹣2x,则l′(x)=ex﹣2.
当x>1时,l′(x)=ex﹣2>e﹣2>0,所以l(x)=h′(x)在(1,+∞)上时单调增函数;
故当x>2时,h′(x)=ex﹣2x>h′(2)=e2﹣4>0,从而h(x)在(2,+∞)上是单调增函数,进而当x>e时,h(x)=ex﹣x2>h(e)=ee﹣e2>0,即当x>e时,ex>x2
当0<a< ![]() ,即
,即 ![]() >e时,f(
>e时,f( ![]() )=
)= ![]() =a(
=a( ![]() )<0,又f(
)<0,又f( ![]() )>0,且函数f(x)在[
)>0,且函数f(x)在[ ![]() ,
, ![]() ]上的图象不间断,所以f(x)在(
]上的图象不间断,所以f(x)在( ![]() ,
, ![]() )上存在零点.
)上存在零点.
又当x> ![]() 时,f′(x)=
时,f′(x)= ![]() ﹣a<0,故f(x)在(
﹣a<0,故f(x)在( ![]() ,+∞)上是单调减函数,所以f(x)在(
,+∞)上是单调减函数,所以f(x)在( ![]() ,+∞)上只有一个零点.
,+∞)上只有一个零点.
综合(i)(ii)(iii),当a≤0或a= ![]() 时,f(x)的零点个数为1,当0<a<
时,f(x)的零点个数为1,当0<a< ![]() 时,f(x)的零点个数为2.
时,f(x)的零点个数为2.
【解析】(1)求导数,利用f(x)在(1,+∞)上是单调减函数,转化为 ![]() ﹣a≤0在(1,+∞)上恒成立,利用g(x)在(1,+∞)上有最小值,结合导数知识,即可求得结论;(2)先确定a的范围,再分类讨论,确定f(x)的单调性,从而可得f(x)的零点个数.
﹣a≤0在(1,+∞)上恒成立,利用g(x)在(1,+∞)上有最小值,结合导数知识,即可求得结论;(2)先确定a的范围,再分类讨论,确定f(x)的单调性,从而可得f(x)的零点个数.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为 ,且有
,且有 ,则不等式
,则不等式 的解集为 ( )
的解集为 ( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn=
 ,n∈N* , 其中c为实数.
,n∈N* , 其中c为实数.
(1)若c=0,且b1 , b2 , b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为
的定义域为 ,部分对应值如下表,又知
,部分对应值如下表,又知 的导函数
的导函数 的图象如下图所示:
的图象如下图所示:
-1
0
4
5

1
2
2
1
则下列关于
 的命题:
的命题:①
 为函数
为函数 的一个极大值点;
的一个极大值点;②函数
 的极小值点为2;
的极小值点为2;③函数
 在
在 上是减函数;
上是减函数;④如果当
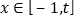 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;⑤当
 时,函数
时,函数 有4个零点.
有4个零点.其中正确命题的序号是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】记
 为虚数集,设
为虚数集,设 ,则下列类比所得的结论正确的是__________.
,则下列类比所得的结论正确的是__________.①由
 ,类比得
,类比得
②由
 ,类比得
,类比得
③由
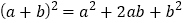 ,类比得
,类比得
④由
 ,类比得
,类比得
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
 的图像向右平衡
的图像向右平衡 个单位长度,再把图象上所有点的横坐标伸长到原来的
个单位长度,再把图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)得到函数
倍(纵坐标不变)得到函数 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )A.函数
 的最大值为
的最大值为 B.函数
B.函数 的最小正周期为
的最小正周期为
C.函数
 的图象关于直线
的图象关于直线 对称D.函数
对称D.函数 在区间
在区间 上单调递增
上单调递增 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)求不等式
 的解集;
的解集;(2)若
 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

