【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表,又知
,部分对应值如下表,又知![]() 的导函数
的导函数![]() 的图象如下图所示:
的图象如下图所示:
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
则下列关于![]() 的命题:
的命题:
①![]() 为函数
为函数![]() 的一个极大值点;
的一个极大值点;
②函数![]() 的极小值点为2;
的极小值点为2;
③函数![]() 在
在![]() 上是减函数;
上是减函数;
④如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4;
的最大值为4;
⑤当![]() 时,函数
时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号是__________.

参考答案:
【答案】②③
【解析】分析:由题意结合导函数与原函数的关系逐一考查所给的命题即可求得结果.
详解:由导数图象可知,当﹣1<x<0或2<x<4时,f′(x)>0,函数单调递增,
当0<x<2或4<x<5,f′(x)<0,函数单调递减,
当x=0和x=4,函数取得极大值f(0)=2,f(4)=2,
当x=2时,函数取得极小值f(2),所以①错误;②③正确;
因为在当x=0和x=4,函数取得极大值f(0)=2,f(4)=2,
要使当x∈[﹣1,t]函数f(x)的最大值是2,
则2≤t≤5,所以t的最大值为5,所以④不正确;
由f(x)=a知,因为极小值f(2)未知,所以无法判断函数y=f(x)﹣a有几个零点,所以⑤不正确.
故答案为:②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=
 ,cosC=
,cosC= 

(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为 ,且有
,且有 ,则不等式
,则不等式 的解集为 ( )
的解集为 ( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn=
 ,n∈N* , 其中c为实数.
,n∈N* , 其中c为实数.
(1)若c=0,且b1 , b2 , b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(﹣1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】记
 为虚数集,设
为虚数集,设 ,则下列类比所得的结论正确的是__________.
,则下列类比所得的结论正确的是__________.①由
 ,类比得
,类比得
②由
 ,类比得
,类比得
③由
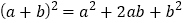 ,类比得
,类比得
④由
 ,类比得
,类比得
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
 的图像向右平衡
的图像向右平衡 个单位长度,再把图象上所有点的横坐标伸长到原来的
个单位长度,再把图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)得到函数
倍(纵坐标不变)得到函数 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )A.函数
 的最大值为
的最大值为 B.函数
B.函数 的最小正周期为
的最小正周期为
C.函数
 的图象关于直线
的图象关于直线 对称D.函数
对称D.函数 在区间
在区间 上单调递增
上单调递增
相关试题

