【题目】设函数![]() 是定义在
是定义在![]() 上的可导函数,其导函数为
上的可导函数,其导函数为![]() ,且有
,且有![]() ,则不等式
,则不等式![]() 的解集为 ( )
的解集为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】分析:根据题意,设g(x)=x2f(x),x>0,求出导数,分析可得g′(x)≥0,则函数g(x)在区间![]() 上为增函数,结合函数g(x)的定义域分析可得:原不等式等价于
上为增函数,结合函数g(x)的定义域分析可得:原不等式等价于![]() ,解可得x的取值范围,即可得答案.
,解可得x的取值范围,即可得答案.
详解:根据题意,设g(x)=x2f(x),x>0,
其导数g′(x)=[x2f(x)]′=2xf(x)+x2f′(x)=x(2f(x)+xf′(x)),
又![]() 且x>0
且x>0
由x(2f(x)+xf′(x))>x2≥0,
则g′(x)g′(x)0,则函数g(x)在区间![]() 上为增函数,
上为增函数,
(x﹣2018)2f(x﹣2018)﹣4f(2)>0
(x﹣2018)2f(x﹣2018)>(2)2f(2)g(x﹣2018)>g(2),
又由函数g(x)在区间(﹣∞,0)上为减函数,
则有![]() ,
,
解可得:x![]() 2020,
2020,
即不等式![]() 的解集为
的解集为![]() ;
;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知变量
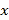 之间的线性回归方程为
之间的线性回归方程为 ,且变量
,且变量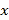 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )x
6
8
10
12
y
6
m
3
2
A. 变量
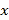 之间呈现负相关关系
之间呈现负相关关系B.
 的值等于5
的值等于5C. 变量
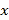 之间的相关系数
之间的相关系数
D. 由表格数据知,该回归直线必过点(9,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列和期望E(X).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=
 ,cosC=
,cosC= 

(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn=
 ,n∈N* , 其中c为实数.
,n∈N* , 其中c为实数.
(1)若c=0,且b1 , b2 , b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为
的定义域为 ,部分对应值如下表,又知
,部分对应值如下表,又知 的导函数
的导函数 的图象如下图所示:
的图象如下图所示:
-1
0
4
5

1
2
2
1
则下列关于
 的命题:
的命题:①
 为函数
为函数 的一个极大值点;
的一个极大值点;②函数
 的极小值点为2;
的极小值点为2;③函数
 在
在 上是减函数;
上是减函数;④如果当
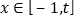 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;⑤当
 时,函数
时,函数 有4个零点.
有4个零点.其中正确命题的序号是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(﹣1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
相关试题

