【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
参考答案:
【答案】
(1)证明:∵sinB(tanA+tanC)=tanAtanC
∴sinB( ![]() )=
)= ![]()
∴sinB ![]() =
= ![]()
∴sinB(sinAcosC+sinCcosA)=sinAsinc
∴sinBsin(A+C)=sinAsinC,
∵A+B+C=π
∴sin(A+C)=sinB
即sin2B=sinAsinC,
由正弦定理可得:b2=ac,
所以a,b,c成等比数列.
(2)解:若a=1,c=2,则b2=ac=2,
∴ ![]() ,
,
∵0<B<π
∴sinB= ![]()
∴△ABC的面积 ![]()
【解析】(1)由已知,利用三角函数的切化弦的原则可得,sinB(sinAcosC+sinCcosA)=sinAsinC,利用两角和的正弦公式及三角形的内角和公式代入可得sin2B=sinAsinC,由正弦定理可证(2)由已知结合余弦定理可求cosB,利用同角平方关系可求sinB,代入三角形的面积公式S= ![]() 可求.
可求.
【考点精析】认真审题,首先需要了解等比数列的基本性质({an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}中,a1=1,a3=﹣3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=﹣35,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC=
 .
.
(1)求角A;
(2)若a=2 ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+6.
(1)当a=5时,解不等式f(x)<0;
(2)若不等式f(x)>0的解集为R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列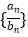 的前n项和Sn .
的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
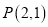 作直线
作直线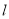 分别交
分别交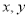 轴的正半轴于
轴的正半轴于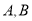 两点.
两点.(Ⅰ)当
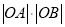 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线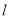 的方程;
的方程;(Ⅱ)当
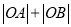 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线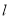 的方程;
的方程;(Ⅲ)当
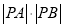 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线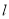 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
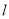 的参数方程为
的参数方程为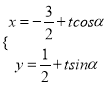 (
(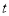 为参数),以
为参数),以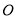 为极点,
为极点, 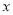 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线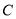 的极坐标方程为
的极坐标方程为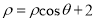 ,(
,( 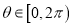 )
)(1)写出直线
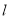 经过的定点的直角坐标,并求曲线
经过的定点的直角坐标,并求曲线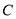 的普通方程;
的普通方程;(2)若
 ,求直线
,求直线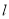 的极坐标方程,以及直线
的极坐标方程,以及直线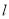 与曲线
与曲线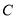 的交点的极坐标.
的交点的极坐标.
相关试题

