【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
参考答案:
【答案】
(1)解:在△ABC中,∵cosBcosC﹣sinBsinC= ![]() ,
,
∴cos(B+C)= ![]() ,
,
又∵0<B+C<π,
∴B+C= ![]() ,
,
∵A+B+C=π,
∴A= ![]()
(2)解:由余弦定理a2=b2+c2﹣2bccosA,
得(2 ![]() )2=(b+c)2﹣2bc﹣2bccos
)2=(b+c)2﹣2bc﹣2bccos ![]() ,
,
把b+c=4代入得:12=16﹣2bc+bc,
整理得:bc=4,
则△ABC的面积S= ![]() bcsinA=
bcsinA= ![]() ×4×
×4× ![]() =
= ![]()
【解析】(1)已知等式左边利用两角和与差的余弦函数公式化简,求出cos(B+C)的值,确定出B+C的度数,即可求出A的度数;(2)利用余弦定理列出关系式,再利用完全平方公式变形,将a与b+c的值代入求出bc的值,再由sinA的值,利用三角形面积公式即可求出三角形ABC面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
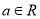 ,若
,若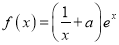 在区间
在区间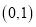 上有且只有一个极值点,则
上有且只有一个极值点,则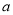 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
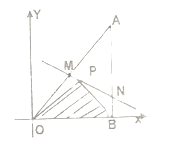
查看答案和解析>>【题目】如图所示,将一块直角三角形木板
 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知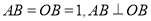 ,点
,点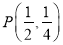 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点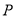 的任一直线
的任一直线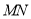 将三角形木板锯成
将三角形木板锯成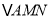 .设直线
.设直线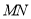 的斜率为
的斜率为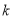 .
.
(Ⅰ)求点
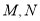 的坐标及直线
的坐标及直线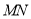 的斜率
的斜率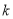 的范围;
的范围;(Ⅱ)令
 的面积为
的面积为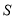 ,试求出
,试求出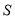 的取值范围;
的取值范围;(Ⅲ)令(Ⅱ)中
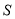 的取值范围为集合
的取值范围为集合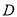 ,若
,若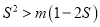 对
对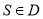 恒成立,求
恒成立,求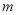 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}中,a1=1,a3=﹣3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=﹣35,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+6.
(1)当a=5时,解不等式f(x)<0;
(2)若不等式f(x)>0的解集为R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB(tanA+tanC)=tanAtanC.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列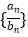 的前n项和Sn .
的前n项和Sn .
相关试题

