【题目】对一批底部周长属于[80,130](单位:cm)的树木进行研究,从中随机抽出200株树木并测出其底部周长,得到频率分布直方图如图所示,由此估计,这批树木的底部周长的众数是cm,中位数是cm,平均数是cm. 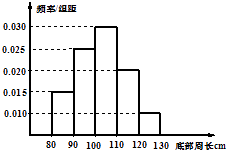
参考答案:
【答案】105;![]() ;103.5
;103.5
【解析】解:①根据频率分布直方图,得;
批树木的底部周长的众数落在100~110之间,取平均数,
故众数是105,
②根据频率分布直方图,得;
数据落在[80,90)的频数是30,
数据落在[90,100)的频数是50,
数据落在[100,110)的频数是60,
数据落在[110,120)的频数是40,
数据落在[120,130)的频数是20,
30+50+60=140>100,30+50=80<100,
∴令0.15+0.25+0.03(x﹣100)=0.5,解得:x= ![]() ,
,
③根据频率分布直方图,得:![]() =85×0.15+95×0.25+105×0.3+115×0.2+125×0.1=103.5
=85×0.15+95×0.25+105×0.3+115×0.2+125×0.1=103.5
所以答案是:105、 ![]() 、103.5.
、103.5.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是
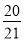 .
.(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量
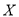 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求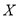 分布列及期望.
分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,如果输入的x∈[﹣2,2],那么输出的y属于( )
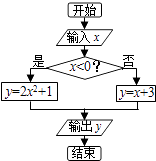
A.[5,9]
B.[3,9]
C.(1,9]
D.(3,5] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  经过点
经过点 ,左右焦点分别为
,左右焦点分别为 、
、 ,圆
,圆 与直线
与直线 相交所得弦长为2.
相交所得弦长为2. (Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
 是椭圆
是椭圆 上不在
上不在 轴上的一个动点,
轴上的一个动点,  为坐标原点,过点
为坐标原点,过点 作
作 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两个不同的点.
两个不同的点.(1)试探究
 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.(2)记
 的面积为
的面积为 ,
,  的面积为
的面积为 ,令
,令 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为
 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A.
 B.
B.  C.
C.  D.
D. 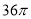
-
科目: 来源: 题型:
查看答案和解析>>【题目】“丁香”和“小花”是好朋友,她们相约本周末去爬歌乐山,并约定周日早上8:00至8:30之间(假定她们在这一时间段内任一时刻等可能的到达)在歌乐山健身步道起点处会合,若“丁香”先到,则她最多等待“小花”15分钟.若“小花”先到,则她最多等待“丁香”10分钟,若在等待时间内对方到达,则她俩就一起快乐地爬山,否则超过等待时间后她们均不再等候对方而孤独爬山,则“丁香”和“小花”快乐地一起爬歌乐山的概率是(用数字作答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得
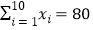 ,
, 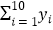 =20,
=20, 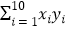 =184,
=184, 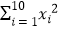 =720.
=720.
(1)求家庭的月储蓄y关于月收入x的线性回归方程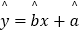 ;
;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: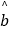 =
= 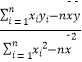 ,
, 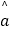 =
= 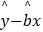 .
.
相关试题

