【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() ,
, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y关于月收入x的线性回归方程 ![]() ;
;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 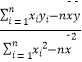 ,
, ![]() =
= ![]() .
.
参考答案:
【答案】
(1)解:由题意知n=10, ![]() ,
, ![]()
又 ![]() ,
, ![]() ,
,
由此得 ![]() ,
, ![]() =
= ![]() =2﹣0.3×8=﹣0.4,
=2﹣0.3×8=﹣0.4,
故所求线性回归方程为 ![]() =0.3x﹣0.4.
=0.3x﹣0.4.
(2)解:将x=7代入回归方程,可以预测该家庭的月储蓄约为 ![]() =0.3×7﹣0.4=1.7(千元).
=0.3×7﹣0.4=1.7(千元).
【解析】1)利用已知条件求出,样本中心坐标,利用参考公式求出b,a,然后求出线性回归方程: ![]() =bx+a;(2)通过x=7,利用回归直线方程,推测该家庭的月储蓄.
=bx+a;(2)通过x=7,利用回归直线方程,推测该家庭的月储蓄.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对一批底部周长属于[80,130](单位:cm)的树木进行研究,从中随机抽出200株树木并测出其底部周长,得到频率分布直方图如图所示,由此估计,这批树木的底部周长的众数是cm,中位数是cm,平均数是cm.
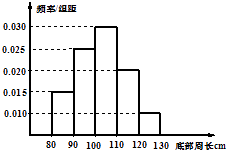
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为
 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A.
 B.
B.  C.
C.  D.
D. 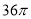
-
科目: 来源: 题型:
查看答案和解析>>【题目】“丁香”和“小花”是好朋友,她们相约本周末去爬歌乐山,并约定周日早上8:00至8:30之间(假定她们在这一时间段内任一时刻等可能的到达)在歌乐山健身步道起点处会合,若“丁香”先到,则她最多等待“小花”15分钟.若“小花”先到,则她最多等待“丁香”10分钟,若在等待时间内对方到达,则她俩就一起快乐地爬山,否则超过等待时间后她们均不再等候对方而孤独爬山,则“丁香”和“小花”快乐地一起爬歌乐山的概率是(用数字作答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的多面体是由一个直平行六面体被平面
 所截后得到的,其中
所截后得到的,其中 ,
, 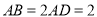 ,
,  .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
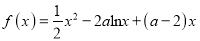 ,
, 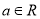 .
. (Ⅰ)当
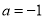 时,求函数
时,求函数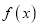 的极值;
的极值;(Ⅱ)当
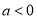 时,讨论函数
时,讨论函数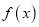 单调性;
单调性;(Ⅲ)是否存在实数
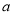 ,对任意的
,对任意的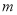 ,
, 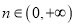 ,且
,且 ,有
,有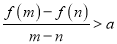 恒成立?若存在,求出
恒成立?若存在,求出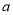 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若关于
 的方程
的方程 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 的取值范围.
的取值范围.
相关试题

