【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是![]() .
.
(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量![]() 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求![]() 分布列及期望.
分布列及期望.
参考答案:
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ)首先设一班志愿者有![]() 人,那么二班有
人,那么二班有![]() 人,至少有一名一班志愿者的概率就是
人,至少有一名一班志愿者的概率就是![]() ,求出人数后,再计算清扫卫生岗位的3人中恰好一班1人,二班2人的概率;(Ⅱ)
,求出人数后,再计算清扫卫生岗位的3人中恰好一班1人,二班2人的概率;(Ⅱ) ![]() 可取的数值为0,1,2,3,根据超几何分布写出其概率
可取的数值为0,1,2,3,根据超几何分布写出其概率![]() 和分布列.
和分布列.
试题解析:(Ⅰ)记“至少一名一班志愿者被分到运送矿泉水岗位”为事件![]() ,则
,则![]() 的对立事件为“没有一班志愿者被分到运送矿泉水岗位”,
的对立事件为“没有一班志愿者被分到运送矿泉水岗位”,
设有一班志愿者![]() 个,
个, ![]() ,那么
,那么![]() ,解得
,解得![]() ,即来自一班的志愿者有5人,来自二班志愿者4人;
,即来自一班的志愿者有5人,来自二班志愿者4人;
记“清扫卫生岗位恰好一班1人,二班2人”为事件![]() ,
,
那么![]() ,
,
所有清扫卫生岗位恰好一班1人,二班2人的概率是![]() .
.
(Ⅱ)![]() 的所有可能值为0,1,2,3.
的所有可能值为0,1,2,3.
![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 的分布列为
的分布列为
|
| 1 | 2 | 3 |
|
|
|
|
|
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】路灯距地面8 m,一个身高为1.6 m的人以84 m/min的速度在地面上从路灯在地面上射影点C沿某直线离开路灯.
(1)求身影的长度y与人距路灯的距离x之间的关系式;
(2)求人离开路灯的第一个10 s内身影的平均变化率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
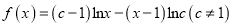 .
.(Ⅰ)讨论
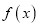 的单调性;
的单调性;(Ⅱ)设
 ,证明:当
,证明:当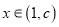 时,
时, 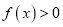 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店会员活动日.
(Ⅰ)随机抽取50名会员对商场进行综合评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
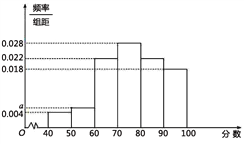
(1)求频率分布直方图中的值;
(2)估计会员对商场的评分不低于80的概率.
(Ⅱ)采取摸球兑奖的方式对会员进行返代金券活动,每位会员从一个装有5个标有面值的球(2个所标的面值为300元,其余3个均为100元)的袋中一次性随机摸出2个球,球上所标的面值之和为该会员所获的代金券金额.求某会员所获得奖励超过400元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,如果输入的x∈[﹣2,2],那么输出的y属于( )
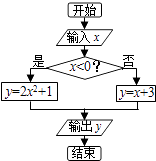
A.[5,9]
B.[3,9]
C.(1,9]
D.(3,5] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  经过点
经过点 ,左右焦点分别为
,左右焦点分别为 、
、 ,圆
,圆 与直线
与直线 相交所得弦长为2.
相交所得弦长为2. (Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
 是椭圆
是椭圆 上不在
上不在 轴上的一个动点,
轴上的一个动点,  为坐标原点,过点
为坐标原点,过点 作
作 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两个不同的点.
两个不同的点.(1)试探究
 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.(2)记
 的面积为
的面积为 ,
,  的面积为
的面积为 ,令
,令 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对一批底部周长属于[80,130](单位:cm)的树木进行研究,从中随机抽出200株树木并测出其底部周长,得到频率分布直方图如图所示,由此估计,这批树木的底部周长的众数是cm,中位数是cm,平均数是cm.
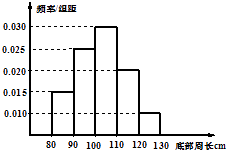
相关试题

