【题目】2018年6月14日,第二十一届世界杯尼球赛在俄罗斯拉开了帷幕,某大学在二年级作了问卷调查,从该校二年级学生中抽取了![]() 人进行调查,其中女生中对足球运动有兴趣的占
人进行调查,其中女生中对足球运动有兴趣的占![]() ,而男生有
,而男生有![]() 人表示对足球运动没有兴趣.
人表示对足球运动没有兴趣.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对足球是否有兴趣与性别有关”?
的把握认为“对足球是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 |
| ||
女 | |||
合计 |
(2)若将频率视为概率,现再从该校二年级全体学生中,采用随机抽样的方法每饮抽取![]() 名学生,抽取
名学生,抽取![]() 次,记被抽取的
次,记被抽取的![]() 名学生中对足球有兴趣的人数为
名学生中对足球有兴趣的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
![]()
参考答案:
【答案】(1)有;(2)![]() .
.
【解析】分析:(1)根据已知数据完成2×2列联表,计算![]() ,判断有
,判断有![]() 的把握认为“对足球有兴趣与性别有关”.(2)先求得从大二学生中抽取一名学生对足球有兴趣的概率是
的把握认为“对足球有兴趣与性别有关”.(2)先求得从大二学生中抽取一名学生对足球有兴趣的概率是![]() ,再利用二项分布求
,再利用二项分布求![]() 的分布列和数学期望.
的分布列和数学期望.
详解:(1)根据已知数据得到如下列联表:
有兴趣 | 没有兴趣 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
根据列联表中的数据,得到![]() ,所以有
,所以有![]() 的把握认为“对足球有兴趣与性别有关”.
的把握认为“对足球有兴趣与性别有关”.
(2)由列联表中数据可知,对足球有兴趣的学生频率是![]() ,将频率视为概率,
,将频率视为概率,
即从大二学生中抽取一名学生对足球有兴趣的概率是![]() ,
,
有题意知![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
从而![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若
,若 是函数
是函数 的唯一极值点,则实数
的唯一极值点,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B. 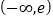 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种农作物可以生长在滩涂和盐碱地,它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度
 对亩产量
对亩产量 (吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:海水浓度






亩产量
 (吨)
(吨)




残差






绘制散点图发现,可以用线性回归模型拟合亩产量
 (吨)与海水浓度
(吨)与海水浓度 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得 与
与 之间的线性回归方程为
之间的线性回归方程为 .
.(1)求
 的值;
的值;(2)统计学中常用相关指数
 来刻画回归效果,
来刻画回归效果, 越大,回归效果越好,如假设
越大,回归效果越好,如假设 ,就说明预报变量
,就说明预报变量 的差异有
的差异有 是解释变量
是解释变量 引起的.请计算相关指数
引起的.请计算相关指数 (精确到
(精确到 ),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?(附:残差
 ,相关指数
,相关指数 ,其中
,其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 张卡片分别写有数字
张卡片分别写有数字 ,从中任取
,从中任取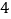 张,可排出不同的四位数个数为( )
张,可排出不同的四位数个数为( )A.
 B.
B. 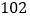 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有
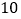 个大小相同的黑球和白球.已知从袋中任意摸出
个大小相同的黑球和白球.已知从袋中任意摸出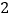 个球,至少得到
个球,至少得到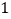 个白球的概率是
个白球的概率是 .
.(1)求白球的个数;
(2)从袋中任意摸出
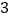 个球,记得到白球的个数为
个球,记得到白球的个数为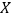 ,求随机变量
,求随机变量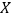 的分布列和数学期望.
的分布列和数学期望.
相关试题

