【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
参考答案:
【答案】(1)a=-5,A=![]() ,B={-5,2}.(2)
,B={-5,2}.(2)![]()
【解析】
(1)根据题意,A∩B={2};有![]() ,即2是2x2+ax+2=0的根,代入可得a=-5,进而分别代入并解2x2+ax+2=0与x2+3x+2a=0可得
,即2是2x2+ax+2=0的根,代入可得a=-5,进而分别代入并解2x2+ax+2=0与x2+3x+2a=0可得![]() ;
;
(2)根据题意,U=A∪B,由(1)可得![]() ;可得全集U,进而可得UA,UB,由并集的定义可得UA)∪(UB)。
;可得全集U,进而可得UA,UB,由并集的定义可得UA)∪(UB)。
(1)由交集的概念易得2是方程2x2+ax+2=0与x2+3x+2a=0的公共解,
则a=-5,此时A=![]() ,B={-5,2}.
,B={-5,2}.
(2)由并集的概念易得U=A∪B=![]() .
.
由补集的概念易得UA={-5},UB=![]() ,
,
所以(UA)∪(UB)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年6月14日,第二十一届世界杯尼球赛在俄罗斯拉开了帷幕,某大学在二年级作了问卷调查,从该校二年级学生中抽取了
 人进行调查,其中女生中对足球运动有兴趣的占
人进行调查,其中女生中对足球运动有兴趣的占 ,而男生有
,而男生有 人表示对足球运动没有兴趣.
人表示对足球运动没有兴趣.(1)完成
 列联表,并回答能否有
列联表,并回答能否有 的把握认为“对足球是否有兴趣与性别有关”?
的把握认为“对足球是否有兴趣与性别有关”?有兴趣
没有兴趣
合计
男

女
合计
(2)若将频率视为概率,现再从该校二年级全体学生中,采用随机抽样的方法每饮抽取
 名学生,抽取
名学生,抽取 次,记被抽取的
次,记被抽取的 名学生中对足球有兴趣的人数为
名学生中对足球有兴趣的人数为 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求 的分布列和数学期望.
的分布列和数学期望.附:











-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 张卡片分别写有数字
张卡片分别写有数字 ,从中任取
,从中任取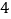 张,可排出不同的四位数个数为( )
张,可排出不同的四位数个数为( )A.
 B.
B. 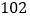 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有
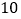 个大小相同的黑球和白球.已知从袋中任意摸出
个大小相同的黑球和白球.已知从袋中任意摸出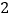 个球,至少得到
个球,至少得到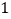 个白球的概率是
个白球的概率是 .
.(1)求白球的个数;
(2)从袋中任意摸出
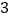 个球,记得到白球的个数为
个球,记得到白球的个数为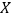 ,求随机变量
,求随机变量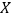 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为
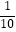 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为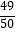 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本
 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.(1)求出2019年的利润
 (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额 成本)
成本)(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
相关试题

