【题目】已知函数 ![]() 的图象过点P(0,2),且在点M(-1,
的图象过点P(0,2),且在点M(-1, ![]() )处的切线方程
)处的切线方程 ![]() 。
。
(1)求函数 ![]() 的解析式;
的解析式;
(2)求函数 ![]() 与
与 ![]() 的图像有三个交点,求a的取值范围。
的图像有三个交点,求a的取值范围。
参考答案:
【答案】
(1)由 的图象经过点P(0,2),知d=2。
所以 ,则
由在 ![]() 处的切线方程是
处的切线方程是 ![]() 知 ,即 。所以3-2b+c=6,-1+b-c+2=1解得b=c=-3。
知 ,即 。所以3-2b+c=6,-1+b-c+2=1解得b=c=-3。
故所求的解析式是 。
(2)因为函数g(x)与 的图像有三个交点
所以 有三个根
即 有三个根
令 ,则 的图像与y=a图像有三个交点。
接下来求 的极大值与极小值(表略)。 的极大值为 的极小值为2
因此
【解析】分析:(1)将点P(0,2)代入函数解析式可得d的值,将 ![]() 代入直线
代入直线 ![]() 可得
可得 ![]() 的值,再由切线方程可知切线的斜率为6,由导数的几何意义可知即
的值,再由切线方程可知切线的斜率为6,由导数的几何意义可知即 ![]() ,解由
,解由 ![]() 和
和 ![]() 组成的方程组可得b,c的值。(2)可将问题转化为
组成的方程组可得b,c的值。(2)可将问题转化为 ![]() 有三个不等的实根问题,将
有三个不等的实根问题,将 ![]() 整理变形可得
整理变形可得 ![]() ,令
,令 ![]() ,则
,则 ![]() 的图像与y=a图像有三个交点。然后对函数
的图像与y=a图像有三个交点。然后对函数 ![]() 求导,令导数等于0求其根。讨论导数的符号,导数正得增区间,导数负得减区间,根据函数的单调性得函数的极值,数形结合分析可得出a的取值范围。
求导,令导数等于0求其根。讨论导数的符号,导数正得增区间,导数负得减区间,根据函数的单调性得函数的极值,数形结合分析可得出a的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数
 的导函数
的导函数  的图象,对此图象,有如下结论:
的图象,对此图象,有如下结论:
①在区间(-2,1)内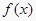 是增函数;
是增函数;
②在区间(1,3)内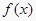 是减函数;
是减函数;
③在 时,
时, 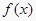 取得极大值;
取得极大值;
④在 时,
时, 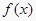 取得极小值。
取得极小值。
其中正确的是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
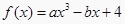 .当x=2时,函数
.当x=2时,函数  取得极值
取得极值 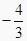 .
.
(1)求函数的解析式;
(2)若函数 =k有3个解,求实数k的取值范围.
=k有3个解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱
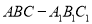 的各条棱长均相等,
的各条棱长均相等, 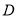 为
为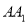 的中点,
的中点, 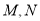 分别是线段
分别是线段 和线段
和线段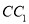 上的动点(含端点),且满足
上的动点(含端点),且满足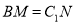 .当
.当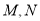 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )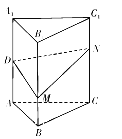
A. 平面
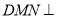 平面
平面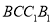 B. 三棱锥
B. 三棱锥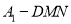 的体积为定值
的体积为定值C.
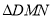 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面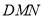 与平面
与平面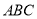 所成的锐二面角范围为
所成的锐二面角范围为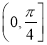
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果  是二次函数,
是二次函数,  的图象开口向上,顶点坐标为(1,
的图象开口向上,顶点坐标为(1,  )
)  ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角  的取值范围是( )
的取值范围是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 的最小值是2
的最小值是2
B. 的最小值是2
的最小值是2
C. 的最小值是
的最小值是 
D. 的最大值是
的最大值是 
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于数列有下列命题:
①数列{an}的前n项和为Sn , 且Sn=an﹣1(a∈R),则{an}为等差或等比数列;
②数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n),
③一个等差数列{an}中,若存在ak+1>ak>0(k∈N*),则对于任意自然数n>k,都有an>0;
④一个等比数列{an}中,若存在自然数k,使akak+1<0,则对于任意n∈N* , 都有anan+1<0,
其中正确命题的序号是 .
相关试题

