【题目】若函数 ![]() .当x=2时,函数
.当x=2时,函数 ![]() 取得极值
取得极值 ![]() .
.
(1)求函数的解析式;
(2)若函数 ![]() =k有3个解,求实数k的取值范围.
=k有3个解,求实数k的取值范围.
参考答案:
【答案】
(1) ,所以 , .即12a-b=0,8a-2b+4= ,由此可解得 ,b=4 ∴
(2) , 所以 在x=-2处取得极大值 ,在x=2处取得极小值 所以
【解析】分析:求函数 ![]() 的定义域;(求函数
的定义域;(求函数 ![]() 的导数
的导数 ![]() ,令
,令 ![]() ,求方程
,求方程 ![]() 的所有实数根;考察
的所有实数根;考察 ![]() 在各实数根左、右的值的符号: ①如果在x0两侧
在各实数根左、右的值的符号: ①如果在x0两侧 ![]() 符号相同,则
符号相同,则 ![]() 不是
不是 ![]() 的极值点;②如果在
的极值点;②如果在 ![]() 附近的左侧
附近的左侧 ![]() ,右侧
,右侧 ![]() ,则
,则 ![]() 是极大值;③如果
是极大值;③如果 ![]() 在
在 ![]() 附近的左侧
附近的左侧 ![]() ,右侧
,右侧 ![]() ,那么
,那么 ![]() 是极小值.
是极小值.
【考点精析】解答此题的关键在于理解函数的极值的相关知识,掌握极值反映的是函数在某一点附近的大小情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
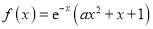 .
.(1)当
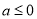 时,求证:
时,求证: 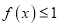 ;
;(2)当
 时,试讨论方程
时,试讨论方程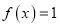 的解的个数.
的解的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.


(1)求
 的值;
的值;(2)该校决定在成绩较好的3、4、5组用分层抽样抽取6名学生进行面试,则每组应各抽多少名学生?
(3)在(2)的前提下,已知面试有4位考官,被抽到的6名学生中有两名被指定甲考官面试,其余4名则随机分配给3位考官中的一位对其进行面试,求这4名学生分配到的考官个数
 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数
 的导函数
的导函数  的图象,对此图象,有如下结论:
的图象,对此图象,有如下结论:
①在区间(-2,1)内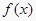 是增函数;
是增函数;
②在区间(1,3)内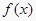 是减函数;
是减函数;
③在 时,
时, 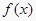 取得极大值;
取得极大值;
④在 时,
时, 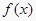 取得极小值。
取得极小值。
其中正确的是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱
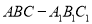 的各条棱长均相等,
的各条棱长均相等, 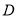 为
为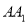 的中点,
的中点, 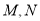 分别是线段
分别是线段 和线段
和线段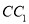 上的动点(含端点),且满足
上的动点(含端点),且满足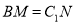 .当
.当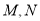 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )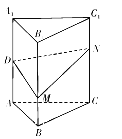
A. 平面
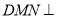 平面
平面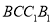 B. 三棱锥
B. 三棱锥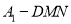 的体积为定值
的体积为定值C.
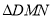 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面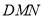 与平面
与平面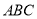 所成的锐二面角范围为
所成的锐二面角范围为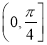
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
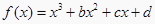 的图象过点P(0,2),且在点M(-1,
的图象过点P(0,2),且在点M(-1, 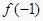 )处的切线方程
)处的切线方程 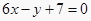 。
。
(1)求函数 的解析式;
的解析式;
(2)求函数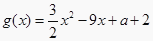 与
与  的图像有三个交点,求a的取值范围。
的图像有三个交点,求a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果  是二次函数,
是二次函数,  的图象开口向上,顶点坐标为(1,
的图象开口向上,顶点坐标为(1,  )
)  ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角  的取值范围是( )
的取值范围是( )
A.
B.
C.
D.
相关试题

